Die ANOVA (Analysis of Variance, auf Deutsch Varianzanalyse) ist eine statistische Methode zur Untersuchung, ob die Mittelwerte mehrerer Gruppen signifikant voneinander abweichen.

Sie wird verwendet, um herauszufinden, ob es Unterschiede in den Mittelwerten von verschiedenen Gruppen gibt, die nicht nur durch Zufall entstanden sind.
In der Statistik, so präzise und klar,
gibt’s ANOVA, wie wunderbar.
Vergleicht die Mittel, testet sacht,
ob zwischen Gruppen ein Unterschied erwacht.ANOVA, oh du herrlich Ding,
Statistiker, sie jubeln und singen.
Denn mit dir, so glasklar und fein,
können wir uns der Wahrheit nah sein.-Kleinhirn.eu
Funktionsweise
– Grundidee: Die ANOVA vergleicht die innerhalb der Gruppen vorhandene Streuung (Varianz) mit der zwischen den Gruppen vorhandenen Streuung.
– Nullhypothese (H₀): Alle Gruppen haben den gleichen Mittelwert.
– Alternativhypothese (H₁): Mindestens eine Gruppe unterscheidet sich signifikant in ihrem Mittelwert von den anderen Gruppen.
– Teststatistik: Die ANOVA berechnet das Verhältnis von zwischen-Gruppen-Varianz zur innerhalb-Gruppen-Varianz. Dieses Verhältnis wird als F-Wert bezeichnet. Ein hoher F-Wert deutet auf signifikante Unterschiede zwischen den Gruppen hin.
Arten der ANOVA
1. Einfaktorielle ANOVA: Untersucht, ob der Mittelwert von mehreren Gruppen, die durch einen Faktor (z.B. unterschiedliche Behandlungen) bestimmt werden, signifikant unterschiedlich ist.
2. Mehrfaktorielle ANOVA: Untersucht die Interaktionseffekte von zwei oder mehr unabhängigen Variablen auf eine abhängige Variable.
3. ANOVA mit wiederholten Messungen: Verwendet, wenn die gleiche Gruppe von Subjekten mehrfach unter verschiedenen Bedingungen gemessen wird.
Anwendungsbereiche
– Vergleich von Mittelwerten in Experimenten, z.B. zur Überprüfung der Wirksamkeit verschiedener Behandlungen.
– Analyse von Umfragedaten, um Unterschiede in den Antworten zwischen verschiedenen demografischen Gruppen zu untersuchen.
– Untersuchung von Wechselwirkungen zwischen mehreren Faktoren in Experimenten.
Voraussetzungen
– Unabhängige Beobachtungen innerhalb der Gruppen.
– Normalverteilung der Daten innerhalb der Gruppen.
-Homogenität der Varianzen (Varianzen der Gruppen sollten ähnlich sein).
Die ANOVA ist ein leistungsfähiges Werkzeug zur statistischen Analyse und wird oft in der Forschung, besonders in den Sozial- und Naturwissenschaften, verwendet.
Wir rechnen mit PSPP mal das Beispiel von Wikipedia zum Thema Varianzanalyse.
Das sind die Daten:
1 45
1 23
1 55
1 32
1 51
1 91
1 74
1 53
1 70
1 84
2 64
2 75
2 95
2 56
2 44
2 130
2 106
2 80
2 87
2 115
Ziel ist es zu prüfen, ob die Mittelwerte der Testergebnisse der Gruppen signifikant voneinander abweichen.
Mögliche Schritte
Hypothesen formulieren:
Nullhypothese (H₀): Die Mittelwerte der drei Gruppen sind gleich.
Alternativhypothese (H₁): Mindestens eine Gruppe unterscheidet sich signifikant.
ANOVA-Test durchführen:
Berechnung der F-Statistik und des p-Wertes mit PSPP
Interpretation:
Wenn der p-Wert kleiner ist als das Signifikanzniveau (z.B. 0,05), gibt es signifikante Unterschiede zwischen den Gruppen.
Dann los. Wir legen zwei Variablen an:
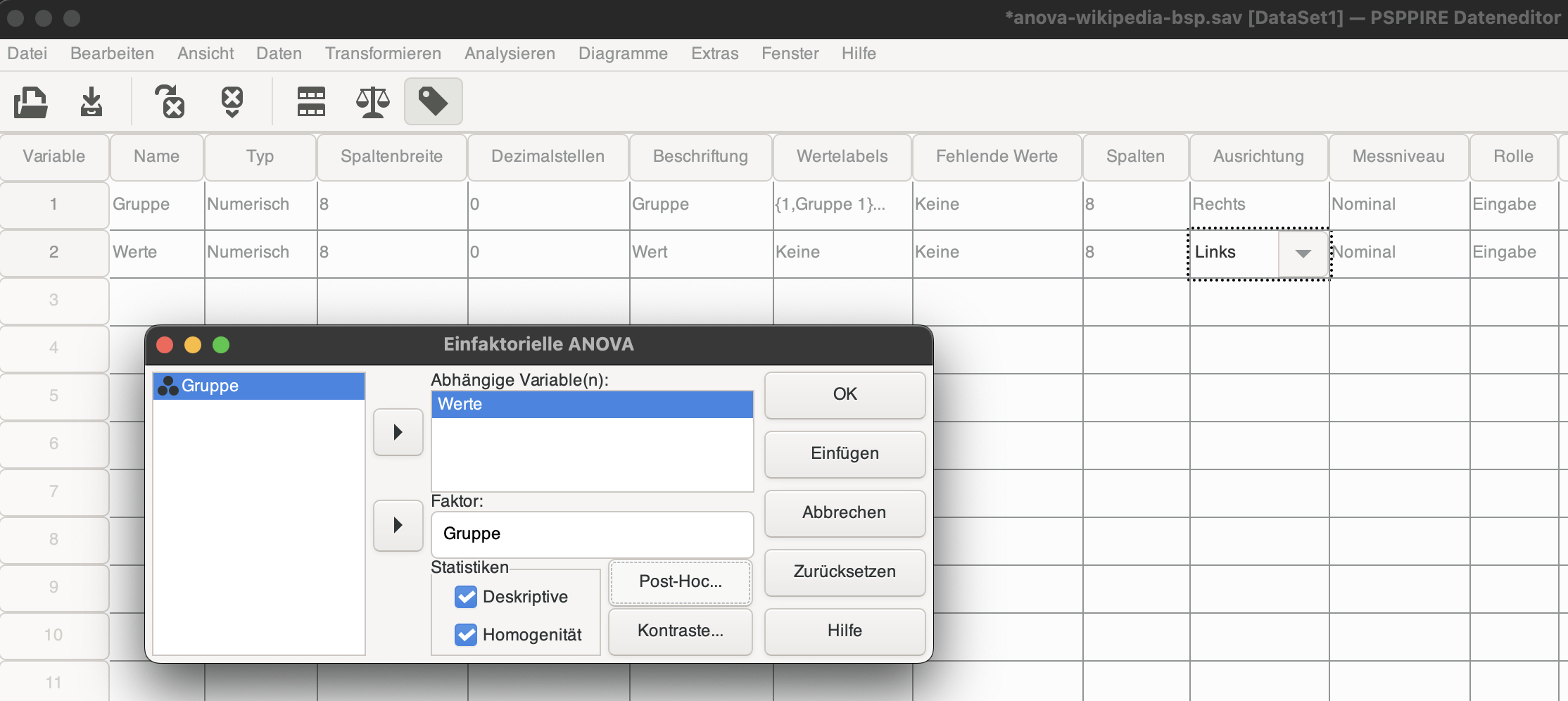
Geben die Daten ein, und berechnen über das Menü: Analysieren – Mittelwert vergleichen – Einfaktorielle ANOVA mit Abhängige Variable: Werte und Faktor: Gruppe. In den Deskriptive Statistik können wir die gewünschten oder alle auswählen:
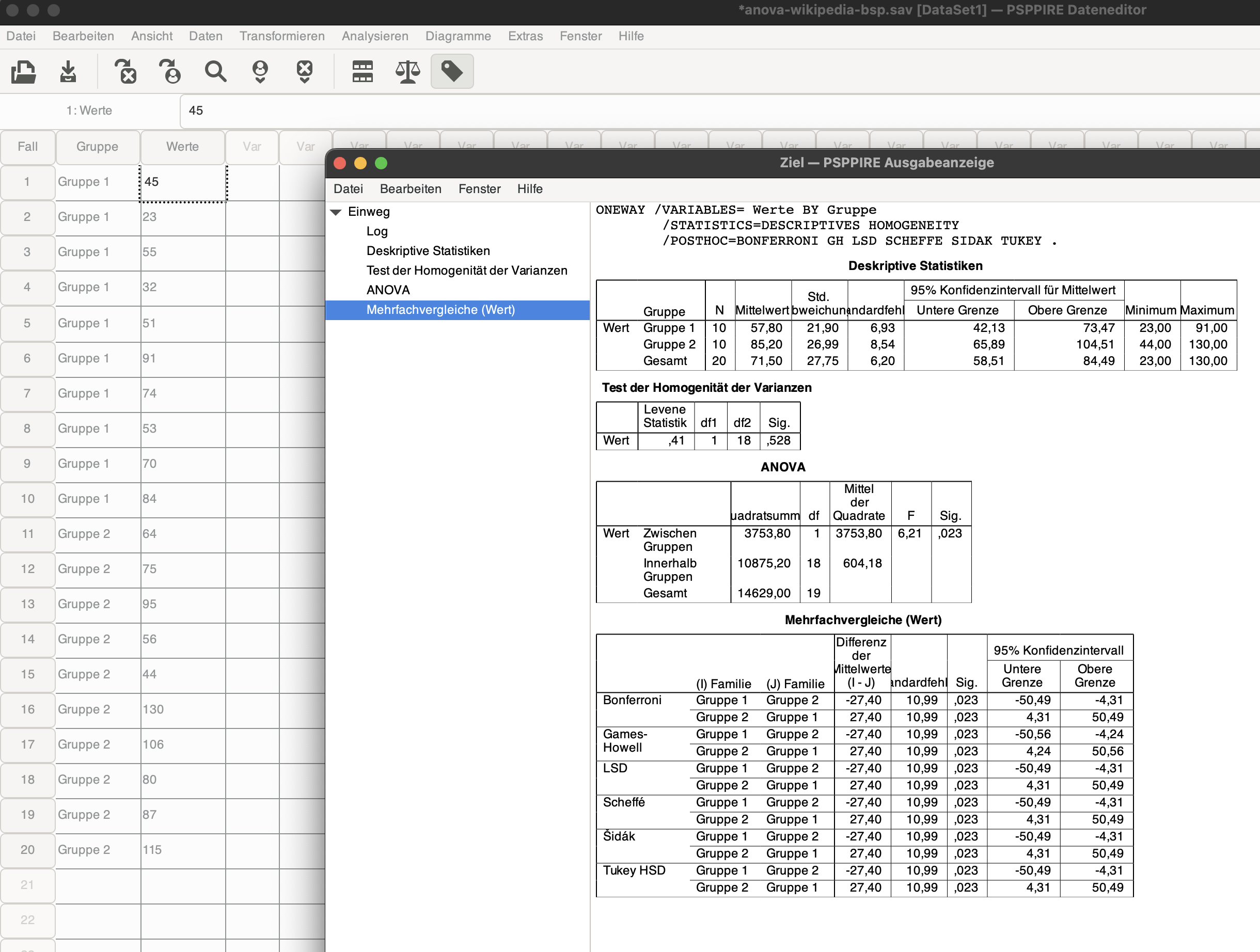
Wer sich die Arbeit nicht machen möchte, kann die Datei auch hier laden anova-wikipedia-bsp.sav und sich das Ergebnis anschauen: wikipedia-beispiel.pdf.
Noch zum Abschluss die Voraussetzungen für die Durchführung einer ANOVA-Analyse die wichtig sind, um sicherzustellen, dass die Ergebnisse valide und aussagekräftig sind. Die wichtigsten Voraussetzungen sind:
Unabhängigkeit der Beobachtungen
Die einzelnen Beobachtungen (Datenpunkte) innerhalb und zwischen den Gruppen müssen unabhängig voneinander sein. Es darf keine systematische Abhängigkeit oder Beziehung zwischen den Messwerten geben.
Normalverteilung der Residuen
Die Daten innerhalb jeder Gruppe sollten annähernd normalverteilt sein. Dies wird meist durch die Verteilung der Residuen (Differenzen zwischen den Beobachtungen und dem Gruppenmittelwert) überprüft. Bei größeren Stichproben (n > 30) ist die ANOVA relativ robust gegenüber Abweichungen von der Normalverteilung.
Homogenität der Varianzen (Homoskedastizität)
Die Varianzen der abhängigen Variable sollten in allen Gruppen ungefähr gleich sein. Dies bedeutet, dass die Streuung der Testergebnisse in den verschiedenen Gruppen ähnlich sein sollte. Dies kann beispielsweise mit dem Levene-Test oder Bartlett-Test überprüft werden.
Skalenniveau der Daten
Die abhängige Variable (z.B. Testergebnis) sollte mindestens intervallskaliert sein. Das bedeutet, die Daten sollten numerisch und die Abstände zwischen den Werten gleich sein.
Wenn eine oder mehrere dieser Voraussetzungen verletzt sind, können alternative statistische Methoden wie die nicht-parametrische Kruskal-Wallis-Test verwendet werden.
