Der Cochrans Q-Test ist ein statistischer Test, der in der deskriptiven Statistik und in der medizinischen Forschung verwendet wird, um festzustellen, ob es signifikante Unterschiede zwischen mehr als zwei abhängigen Gruppen oder Bedingungen gibt. Dieser Test wird oft in Verbindung mit wiederholten Messungen oder wiederholten Stichproben (auch als within-subjects oder repeated measures bezeichnet) angewendet, bei denen dieselben Personen oder Elemente in verschiedenen Gruppen oder zu verschiedenen Zeitpunkten gemessen werden.

Der Cochrans Q-Test ist ein nichtparametrischer Test und basiert auf der Anzahl der Abweichungen in den verschiedenen Gruppen. Im Wesentlichen vergleicht der Test die Unterschiede zwischen den Gruppen mit den erwarteten Unterschieden, die zufällig auftreten würden. Wenn die beobachteten Unterschiede zwischen den Gruppen signifikant größer sind als die zufällig erwarteten Unterschiede, weist dies auf signifikante Unterschiede zwischen den Gruppen hin.
Die Hypothesen, die mit dem Cochrans Q-Test getestet werden, sind normalerweise wie folgt:
– Nullhypothese (H0): Es gibt keine signifikanten Unterschiede zwischen den Gruppen.
– Alternativhypothese (H1): Es gibt signifikante Unterschiede zwischen den Gruppen.
Der Cochrans Q-Test ist besonders nützlich, wenn Sie über mehrere Kategorien oder Messzeitpunkte verfügen und überprüfen möchten, ob es signifikante Unterschiede zwischen ihnen gibt. Wenn der Cochrans Q-Test signifikant ist, weist dies darauf hin, dass zumindest eine der Gruppen signifikant von den anderen abweicht. In einem solchen Fall können post hoc-Tests oder weitere Analysen durchgeführt werden, um festzustellen, welche Gruppen voneinander abweichen.
Beim Cochrans Q-Test ist die Testvariable binär skaliert, z.B. Krankheit: Krank = 1 und Nicht Krank = 0 und es gibt mindestens 3 Zeitpunkte (z.B. t1,t2,t3)
So nun zu einem Beispiel mit PSPP.
Der Cochrans Q-Test in PSPP testet verbundene Stichproben (selbe Probanden zu verschiedenen Zeitpunkten) hinsichtlich eines binären Merkmals und ob sich jenes geändert hat. Beispielsweise wurde bei Menschen eine Krankheit diagnostiziert (t1). Nach einer ersten Behandlung werden sie erneut speziell auf diese Krankheit untersucht und entweder ist die Krankheit immer noch vorhanden oder eben nicht mehr (t2). Eine erneute Behandlung muss nicht erfolgen, es wird aber ein zweites Mal gemessen, da gewisse Behandlungen bei manchen Menschen erst später anschlagen können (t3). Hierfür ist der Cochran’s Q-Test auf Basis eines Chi 2-Testes entwickelt worden. Er zeigt, ob die Behandlung(en) einen statistisch signifikanten Effekt erzielt hat und prüft dies bei mindestens zwei Messwiederholungen.
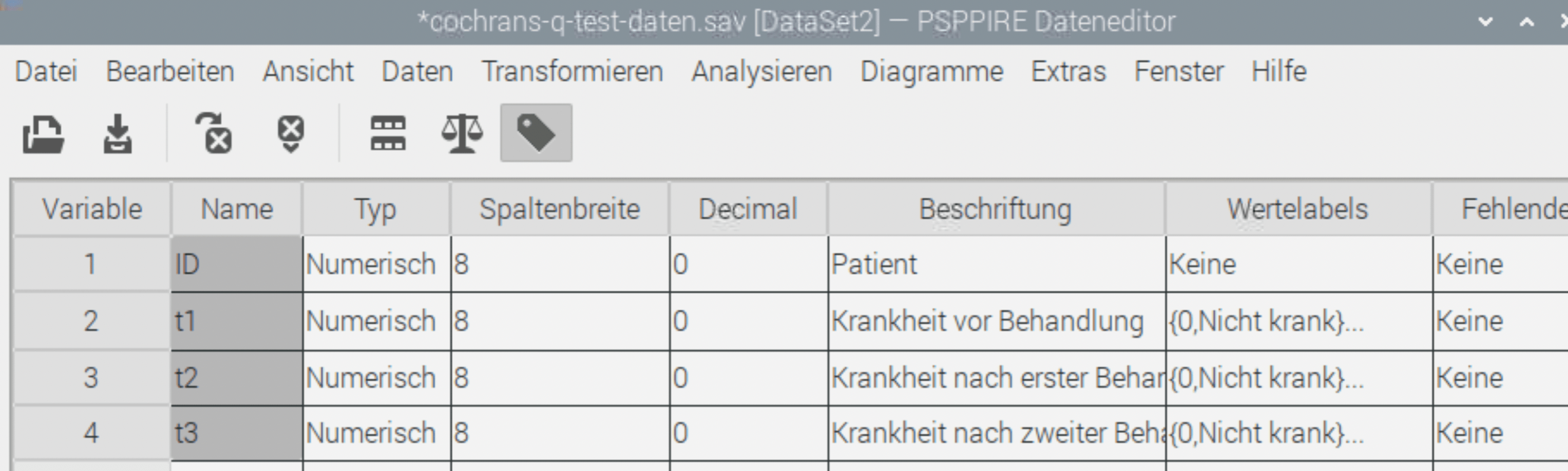
Wir legen diese 4 Numerischen Variablen an.
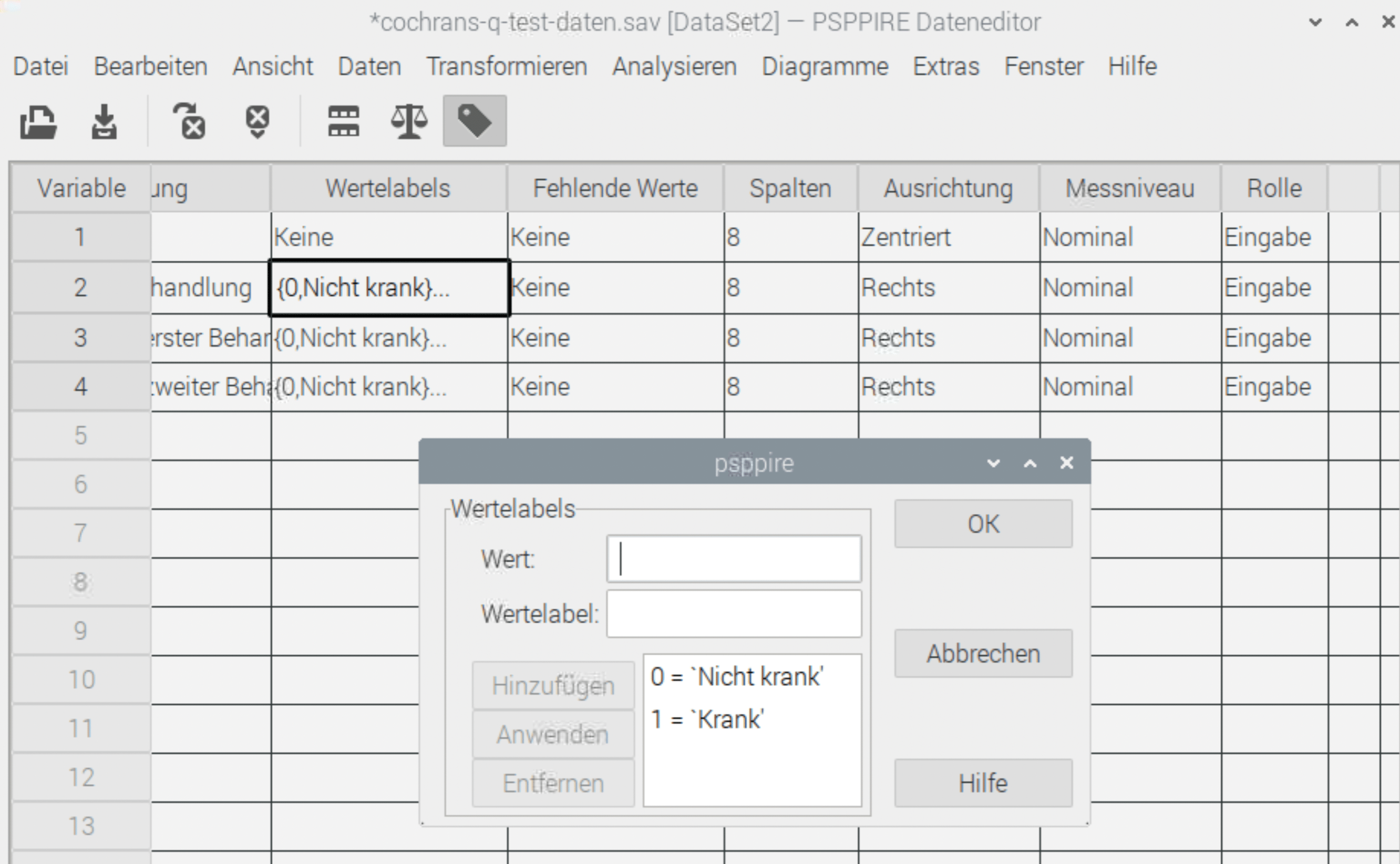
Die 1. ist die ID oder der Patient. t1,t2,t3 sind die Zeitpunkte vor der Behandlung (t1), nach der ersten Behandlung (t2) und nach der zweiten Behandlung (t3). Alle drei bekommen als Wertelabels den Wert 0 = Nicht Krank und 1 = Krank und als Messniveau: Nominal
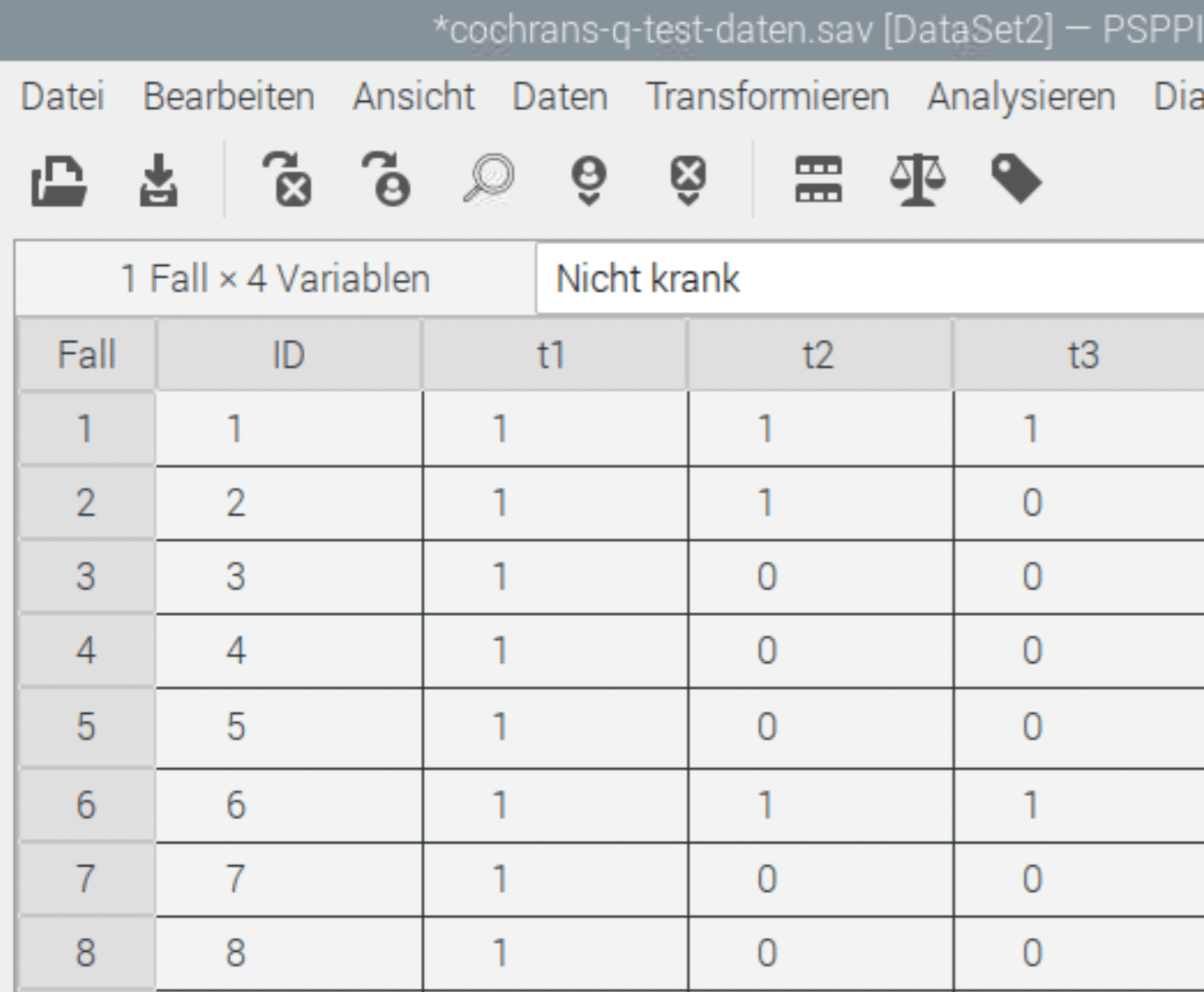
Jetzt geben wir mal 70 Test-Datensätze ein. Z.B.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
1 Krank Krank Krank 2 Krank Krank Nicht krank 3 Krank Nicht krank Nicht krank 4 Krank Nicht krank Nicht krank 5 Krank Nicht krank Nicht krank 6 Krank Krank Krank 7 Krank Nicht krank Nicht krank 8 Krank Nicht krank Nicht krank 9 Krank Krank Krank 10 Krank Nicht krank Nicht krank 11 Krank Krank Krank 12 Nicht krank Nicht krank Nicht krank 13 Nicht krank Nicht krank Nicht krank 14 Nicht krank Nicht krank Nicht krank 15 Nicht krank Nicht krank Nicht krank 16 Krank Krank Nicht krank 17 Krank Krank Krank 18 Krank Nicht krank Nicht krank 19 Nicht krank Nicht krank Nicht krank 20 Nicht krank Nicht krank Nicht krank 21 Krank Nicht krank Nicht krank 22 Krank Nicht krank Nicht krank 23 Krank Nicht krank Nicht krank 24 Nicht krank Nicht krank Nicht krank 25 Nicht krank Nicht krank Nicht krank 26 Krank Krank Nicht krank 27 Krank Krank Krank 28 Krank Nicht krank Nicht krank 29 Krank Nicht krank Nicht krank 30 Krank Nicht krank Nicht krank 31 Krank Krank Nicht krank 32 Krank Nicht krank Nicht krank 33 Krank Nicht krank Nicht krank 34 Krank Krank Krank 35 Krank Nicht krank Nicht krank 36 Krank Krank Krank 37 Nicht krank Nicht krank Nicht krank 38 Nicht krank Nicht krank Nicht krank 39 Nicht krank Nicht krank Nicht krank 40 Nicht krank Krank Nicht krank 41 Krank Krank Krank 42 Nicht krank Nicht krank Nicht krank 43 Krank Nicht krank Nicht krank 44 Nicht krank Nicht krank Nicht krank 45 Nicht krank Nicht krank Nicht krank 46 Krank Nicht krank Nicht krank 47 Krank Nicht krank Nicht krank 48 Krank Nicht krank Nicht krank 49 Nicht krank Nicht krank Nicht krank 50 Nicht krank Nicht krank Nicht krank 51 Krank Krank Nicht krank 52 Krank Nicht krank Nicht krank 53 Nicht krank Nicht krank Nicht krank 54 Nicht krank Nicht krank Nicht krank 55 Krank Nicht krank Nicht krank 56 Krank Nicht krank Nicht krank 57 Krank Nicht krank Nicht krank 58 Nicht krank Nicht krank Nicht krank 59 Nicht krank Nicht krank Nicht krank 60 Krank Krank Krank 61 Krank Krank Krank 62 Krank Krank Krank 63 Krank Krank Krank 64 Krank Krank Krank 65 Krank Krank Krank 66 Nicht krank Nicht krank Nicht krank 67 Nicht krank Nicht krank Nicht krank 68 Krank Krank Nicht krank 69 Krank Nicht krank Nicht krank 70 Krank Krank Nicht krank |
Hier die Ansicht binär Kodiert:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
1 1 1 1 2 1 1 0 3 1 0 0 4 1 0 0 5 1 0 0 6 1 1 1 7 1 0 0 8 1 0 0 9 1 1 1 10 1 0 0 11 1 1 1 12 0 0 0 13 0 0 0 14 0 0 0 15 0 0 0 16 1 1 0 17 1 1 1 18 1 0 0 19 0 0 0 20 0 0 0 21 1 0 0 22 1 0 0 23 1 0 0 24 0 0 0 25 0 0 0 26 1 1 0 27 1 1 1 28 1 0 0 29 1 0 0 30 1 0 0 31 1 1 0 32 1 0 0 33 1 0 0 34 1 1 1 35 1 0 0 36 1 1 1 37 0 0 0 38 0 0 0 39 0 0 0 40 0 1 0 41 1 1 1 42 0 0 0 43 1 0 0 44 0 0 0 45 0 0 0 46 1 0 0 47 1 0 0 48 1 0 0 49 0 0 0 50 0 0 0 51 1 1 0 52 1 0 0 53 0 0 0 54 0 0 0 55 1 0 0 56 1 0 0 57 1 0 0 58 0 0 0 59 0 0 0 60 1 1 1 61 1 1 1 62 1 1 1 63 1 1 1 64 1 1 1 65 1 1 1 66 0 0 0 67 0 0 0 68 1 1 0 69 1 0 0 70 1 1 0 |
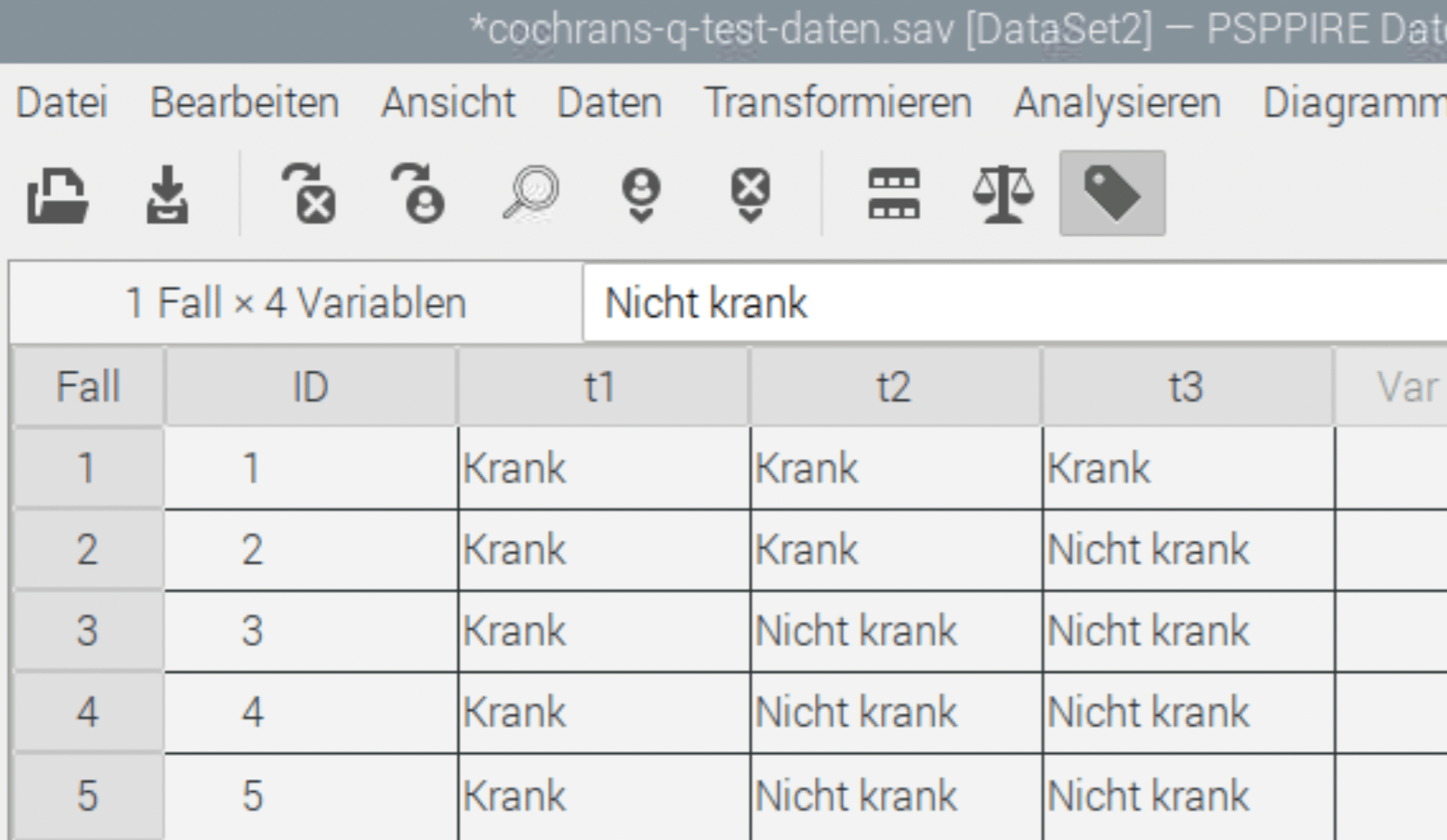
Und als Text:
So, jetzt rechnen wir erst einmal die Häufigkeit aus, über das Menü: Analysieren – Deskriptive Statistiken – Häufigkeit.
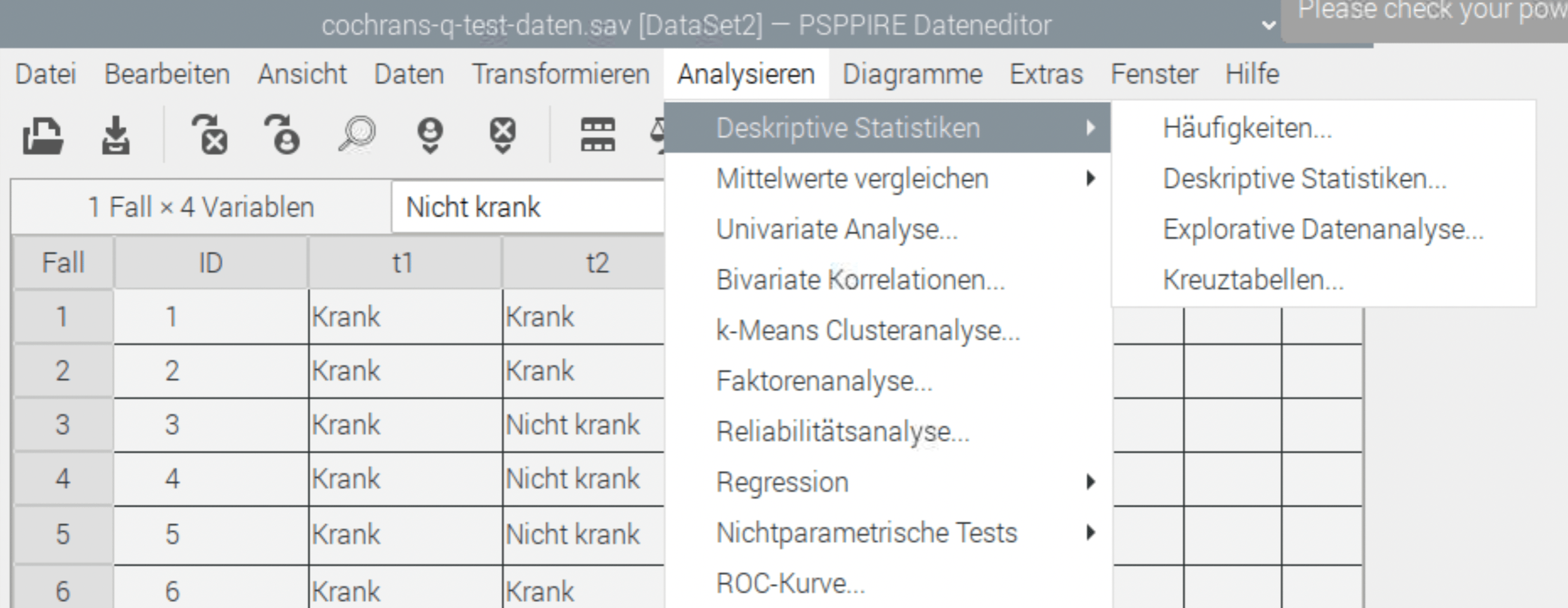
In dem Dialog wählen wir die t1,t2 und t3 aus und klicken auf OK.
Wir erhalten dieses Ergebnis:


und wenn wir im vorherigen Dialog auch Diagramme ausgewählt haben
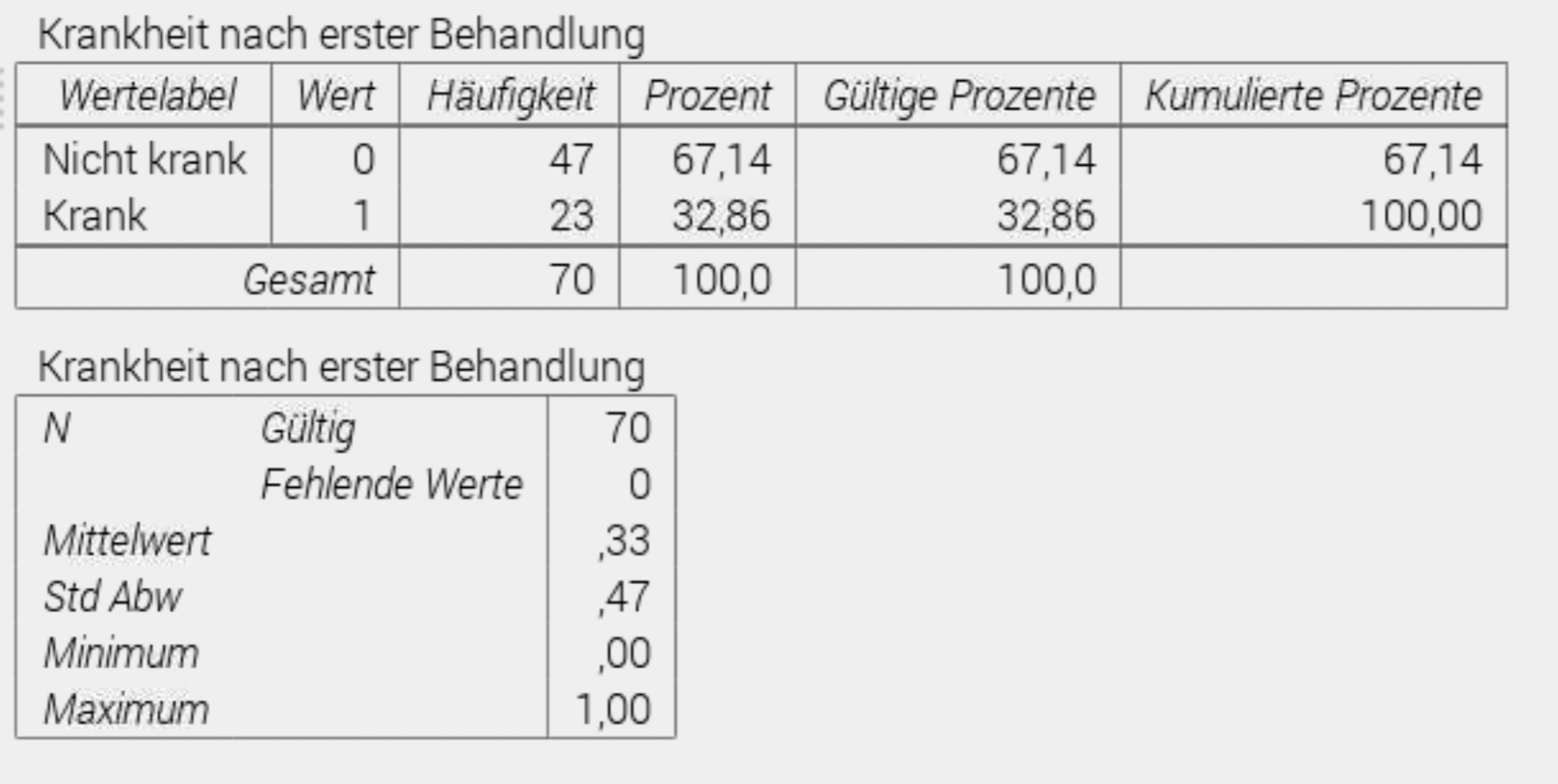
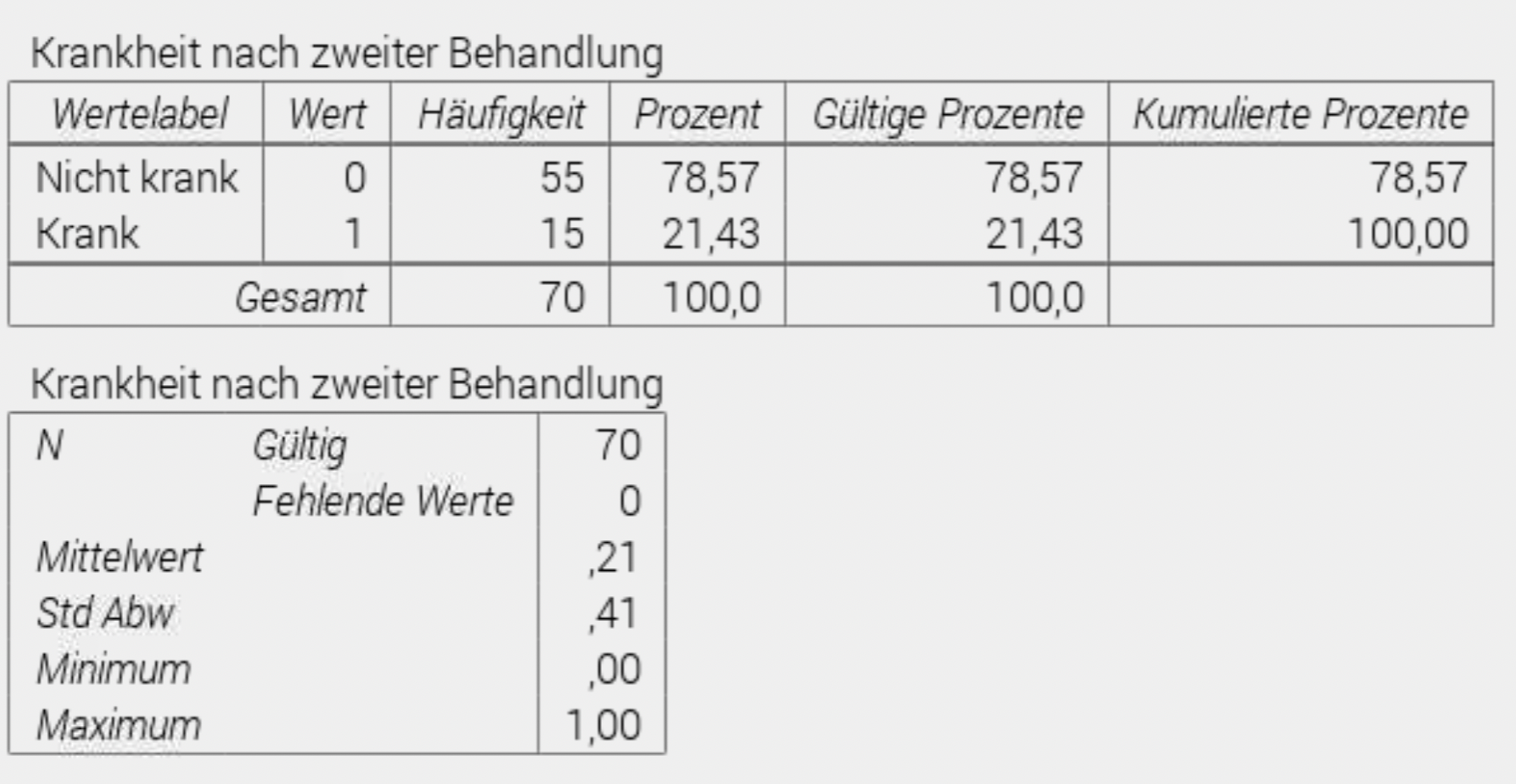
Wir können auch die descriptive Häufigkeit über das Menü: Analysieren – Descriptive Statistiken – Descriptive Statistiken einen schönen Zusammenfassung berechnen:
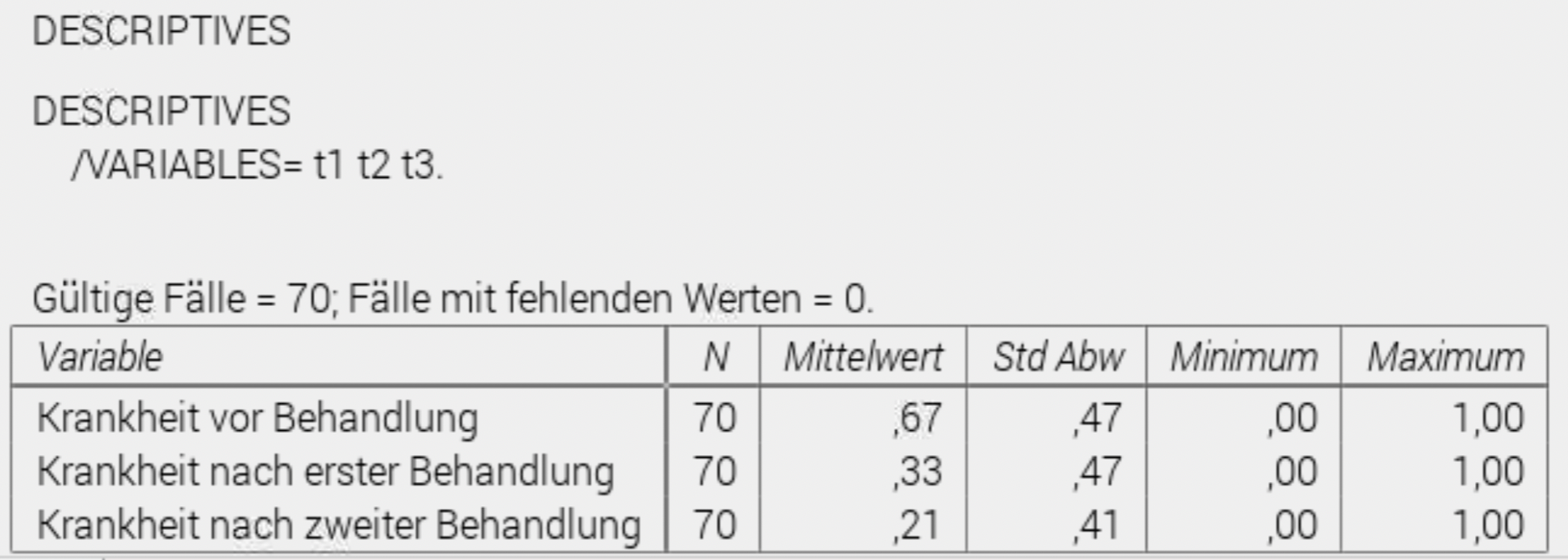
Jetzt kommen wir zu dem eigentlichen gewünschten Cochrans Q-Test.
Wir wählen im Menü: Analysieren – Nichtparametrische Tests – K verbundene Stichproben… aus
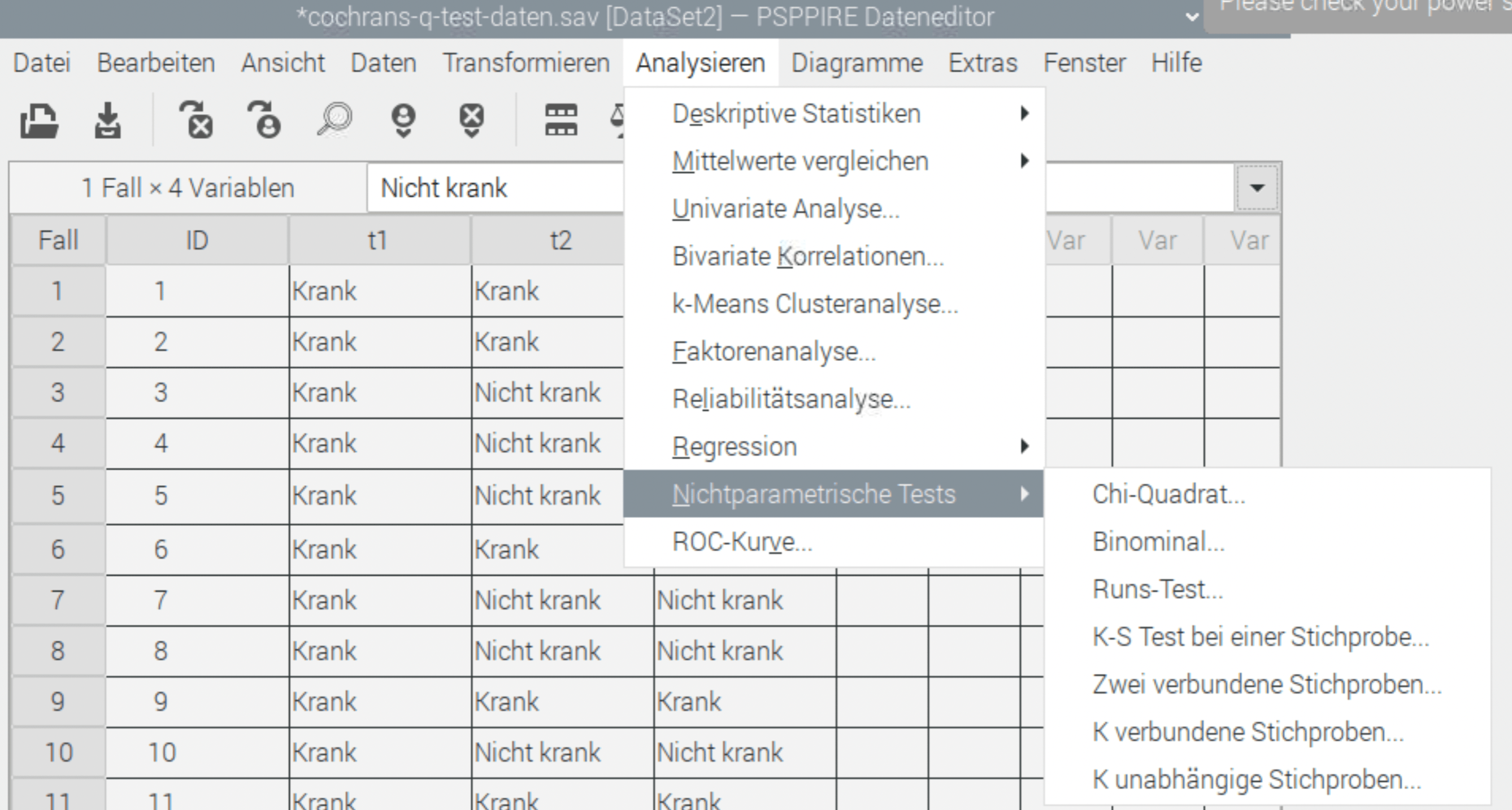
In den Dialog wählen wir die drei Testvariablen und das ist wichtig, die rechte Checkbox: Cochran-Q aus. Dann auf OK:
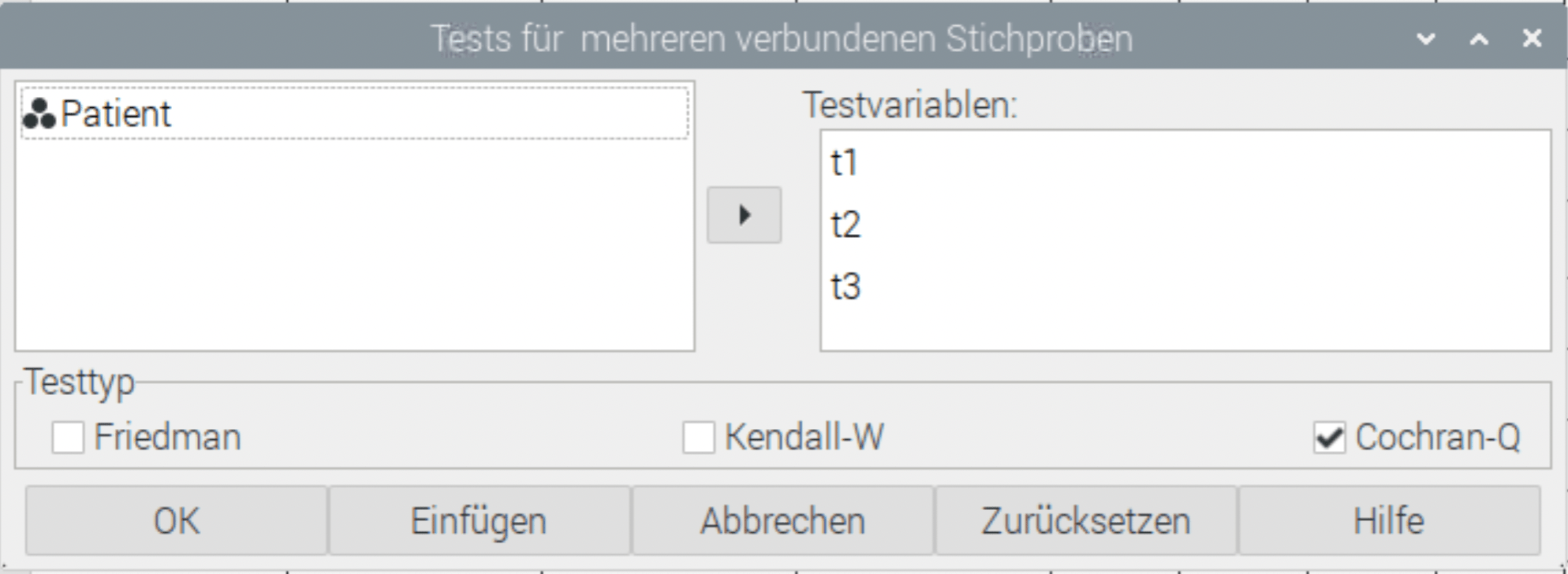
Das Ergebnis des Cochran-Q

Wir können also sehen, das die Erfolge unserer Test-Daten von 47 vor der Behandlung, besser wird auf 23 nach der ersten Behandlung und nach der zweiten Behandlung sogar auf 15. Der Cochrans Q-Test ist schon hoch mit 50,42 und damit kann die Nullhypothese verworfen werden.
Die Asymptotische Signifikanz (Asymp. Sig) wird oft in statistischen Ausgaben und Berichten angegeben und zeigt das Signifikanzniveau (p-Wert) an, das auf den asymptotischen Annahmen basiert. Ein typisches Signifikanzniveau ist beispielsweise 0,05, was bedeutet, dass, wenn „Asymp. Sig“ kleiner als 0,05 ist, die Ergebnisse als statistisch signifikant angesehen werden. Dies impliziert, dass die Wahrscheinlichkeit, dass die beobachteten Unterschiede oder Effekte auf reiner Zufall beruhen, gering ist, und daher die Nullhypothese abgelehnt werden kann.
Die Asymp. Sig. ist bei .000 und damit liegen wir unter .05 sogar unter 0.01 sind damit sehr Signifikant.
Behandlungen haben also aufgrund der Stichproben Signifikanz und sind nicht reiner Zufall.
Das Ergebnis wollen wir nun mit einem Online Rechner validieren.
Die 70 Datensätze von oben mit Semikolon formatiert:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
1;1;1 1;1;0 1;0;0 1;0;0 1;0;0 1;1;1 1;0;0 1;0;0 1;1;1 1;0;0 1;1;1 0;0;0 0;0;0 0;0;0 0;0;0 1;1;0 1;1;1 1;0;0 0;0;0 0;0;0 1;0;0 1;0;0 1;0;0 0;0;0 0;0;0 1;1;0 1;1;1 1;0;0 1;0;0 1;0;0 1;1;0 1;0;0 1;0;0 1;1;1 1;0;0 1;1;1 0;0;0 0;0;0 0;0;0 0;1;0 1;1;1 0;0;0 1;0;0 0;0;0 0;0;0 1;0;0 1;0;0 1;0;0 0;0;0 0;0;0 1;1;0 1;0;0 0;0;0 0;0;0 1;0;0 1;0;0 1;0;0 0;0;0 0;0;0 1;1;1 1;1;1 1;1;1 1;1;1 1;1;1 1;1;1 0;0;0 0;0;0 1;1;0 1;0;0 1;1;0 |
auf der Seite eingeben und den Cochrans Q-Test in der Combobox auswählen. Dann auf den Start Button clicken. Wir kommen auf eine Seite, wo alle drei Spalten mit den Werten angezeigt werden. Dann klicken wir auf „Calculate χ²-score and P-value“ Button. Wir erhalten dieses Ergebnis:

Wir haben nun das gleiche Ergebns 50.42. Super. Das Ergebnis ist mit kleiner .05 sehr Signifikant.
