Der Brier-Wert ist ein effizientes und einfaches Maß zur Bewertung der Genauigkeit probabilistischer Vorhersagen. Durch die Kombination aus einfacher Berechnung und aussagekräftiger Analyse ist er ein weit verbreitetes Werkzeug in der Statistik und im maschinellen Lernen.
In der Praxis hilft er, die Qualität von Vorhersagen quantitativ zu bewerten und kann zur Verbesserung von Modellen und Algorithmen beitragen. Die Bezeichnung „Brier-Wert“ stammt von dem amerikanischen Meteorologen Glenn W. Brier, der das Maß (1950 – VERIFICATION OF FORECASTS EXPRESSED IN TERMS OF PROBABILITY) entwickelte und damit die Grundlage legte.
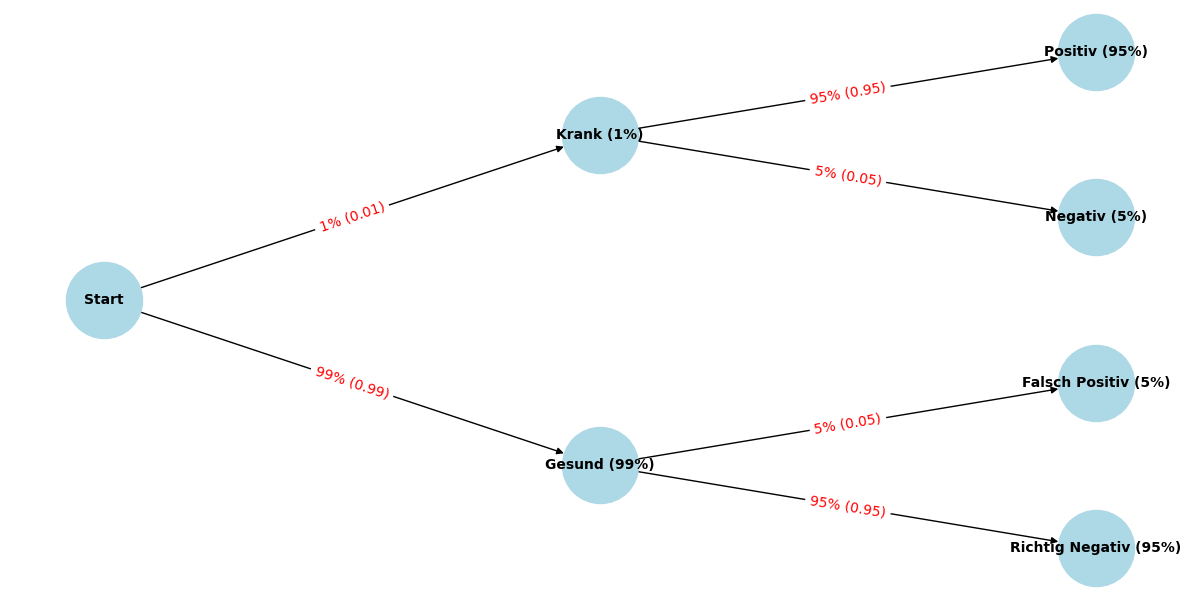
Der Brier-Wert wird häufig in Bereichen wie Meteorologie, Medizin, Finanzwesen, Wahlprognosen und maschinellem Lernen verwendet, um die Genauigkeit von Prognosen zu bewerten. Er ist besonders nützlich bei binären Klassifikationsproblemen, bei denen das Modell Wahrscheinlichkeiten für die Zugehörigkeit zu einer von zwei Klassen liefert (z. B. Regenwahrscheinlichkeit).
Wir erstellen zur Verdeutlichung mal ein JSon Datei mit ein paar Daten von der Reserve Bank of Australia, die bei ihren monatlichen Sitzungen Zinssätze beschließt. Die RBA lässt die Zinssätze im Allgemeinen unverändert, erhöht sie jedoch manchmal und senkt sie manchmal, je nach wirtschaftlicher Lage. Die Daten stammen aus diesem Artikel und wurden von mir in das JSon-Format überführt. „Der Brier-Score (Brier-Wert) nicht nur für Prognostiker“ weiterlesen