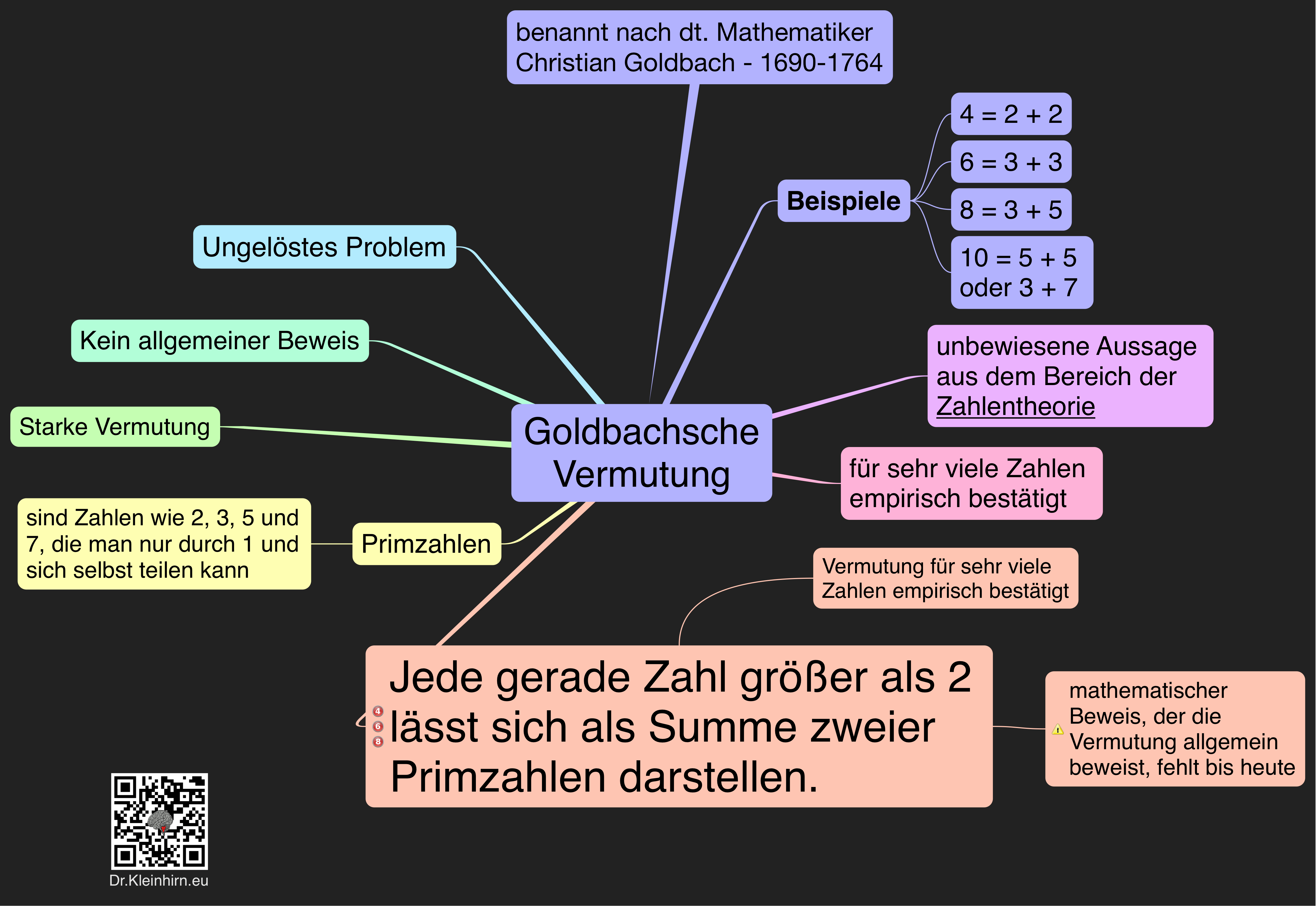
Die Goldbachsche Vermutung ist eine der ältesten ungelösten Probleme in der Mathematik, die der Mathematiker Christian Goldbach 1742 in einem Brief an Leonhard Euler formulierte. Sie besagt:
Jede gerade Zahl größer als 2 lässt sich als Summe zweier Primzahlen darstellen.
Diese Vermutung ist in zwei Formen bekannt:
1. Schwache Goldbachsche Vermutung: Jede ungerade Zahl größer als 5 lässt sich als Summe von drei Primzahlen darstellen. Diese Vermutung wurde 2013 von Harald Helfgott bewiesen.
2. Starke Goldbachsche Vermutung: Jede gerade Zahl größer als 2 lässt sich als Summe von zwei Primzahlen darstellen. Dies ist die berühmtere und unbewiesene Form der Vermutung.
Beispiele:
4 = 2 + 2
6 = 3 + 3
8 = 3 + 5
10 = 5 + 5 oder 3 + 7
Obwohl die Vermutung für sehr viele Zahlen empirisch bestätigt wurde, ist bislang kein allgemeiner Beweis bekannt, der für alle geraden Zahlen gilt. Mathematiker haben die Vermutung für sehr große Zahlen durch Computertests überprüft, aber ein mathematischer Beweis, der die Vermutung allgemein beweist, fehlt bis heute.
Wenn das mal kein Grund ist, ein Java-Programm für die starke Goldbachsche Vermutung zu schreiben, das das überprüft.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
package de.wenzlaff; import java.math.BigInteger; /** * GoldbachsVermutung. * * Starke Goldbachsche Vermutung: Jede gerade Zahl größer als 2 lässt sich als * Summe von zwei Primzahlen darstellen. Dies ist die berühmtere und unbewiesene * Form der Vermutung. * * Beispiele: * * 4 = 2 + 2 * * 6 = 3 + 3 * * 8 = 3 + 5 * * 10 = 5 + 5 oder 3 + 7 * * Anm.: Mit Ausnahme der Zahl 2 sind alle Primzahlen ungerade * * @author Thomas Wenzlaff */ public class GoldbachsVermutung { public static void main(String[] args) { if (args.length != 2) { System.out.println("Bitte zwei Parameter eingeben: eine obere Grenze und eine Startzahl."); return; } try { BigInteger obergrenze = new BigInteger(args[0]); BigInteger zwei = BigInteger.valueOf(2); BigInteger startzahl = new BigInteger(args[1]); if (obergrenze.compareTo(startzahl) >= 0 && startzahl.compareTo(BigInteger.valueOf(2)) >= 0 && startzahl.mod(zwei).equals(BigInteger.ZERO)) { for (BigInteger zahl = startzahl; zahl.compareTo(obergrenze) <= 0; zahl = zahl.add(zwei)) { boolean ergebnis = pruefeGoldbach(zahl); if (!ergebnis) { String text = "Die Zahl " + zahl + " lässt sich NICHT als Summe zweier Primzahlen darstellen."; System.err.println(text); throw new IllegalArgumentException(text); } } } else { System.out.println("Bitte eine gültige obere Grenze und eine gerade Startzahl größer als 2 eingeben."); } } catch (NumberFormatException e) { System.out.println("Bitte zwei Parameter eingeben: eine obere Grenze und eine Startzahl."); } } // Überprüft, ob eine Zahl als Summe zweier Primzahlen darstellbar ist public static boolean pruefeGoldbach(BigInteger zahl) { BigInteger zwei = BigInteger.valueOf(2); for (BigInteger i = zwei; i.compareTo(zahl.divide(zwei)) <= 0; i = i.add(BigInteger.ONE)) { if (istPrimzahl(i) && istPrimzahl(zahl.subtract(i))) { System.out.println(zahl + " = " + i + " + " + zahl.subtract(i)); return true; } } return false; } // Überprüft, ob eine Zahl eine Primzahl ist public static boolean istPrimzahl(BigInteger zahl) { if (zahl.compareTo(BigInteger.ONE) <= 0) return false; BigInteger sqrtZahl = zahl.sqrt(); for (BigInteger i = BigInteger.valueOf(2); i.compareTo(sqrtZahl) <= 0; i = i.add(BigInteger.ONE)) { if (zahl.mod(i).equals(BigInteger.ZERO)) { return false; } } return true; } } |
Ich starte das Programm mal mit openjdk 21.0.1 und diesen Werten: 1000000000 2
Zusätzlich um den Speicher während des laufes zu analysieren:
|
1 |
-Dcom.sun.management.jmxremote -Dcom.sun.management.jmxremote.port=12345 -Dcom.sun.management.jmxremote.authenticate=false -Dcom.sun.management.jmxremote.ssl=false |
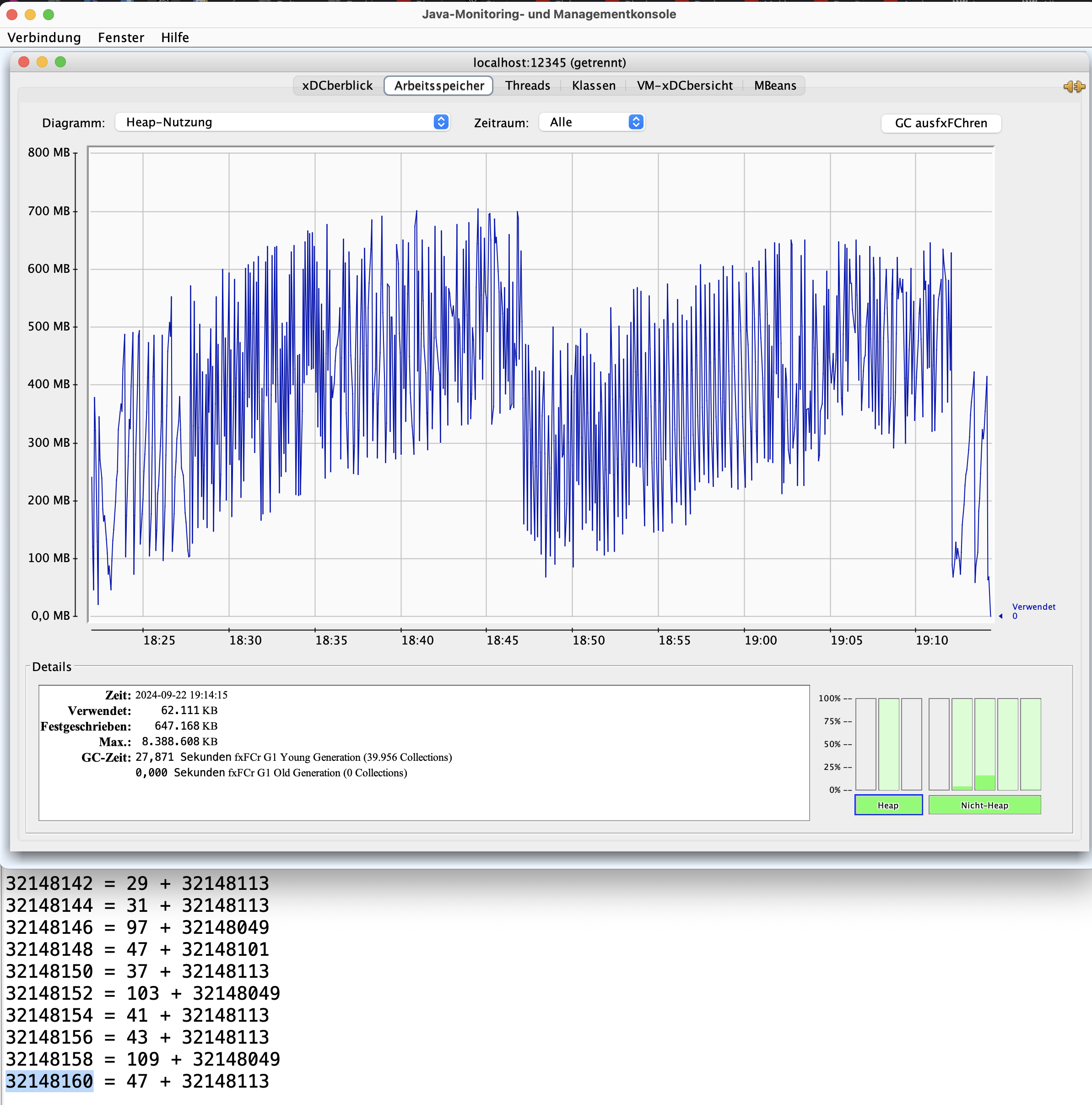
Der Speicher sieht nach ca. einer Stunde Laufzeit so aus:
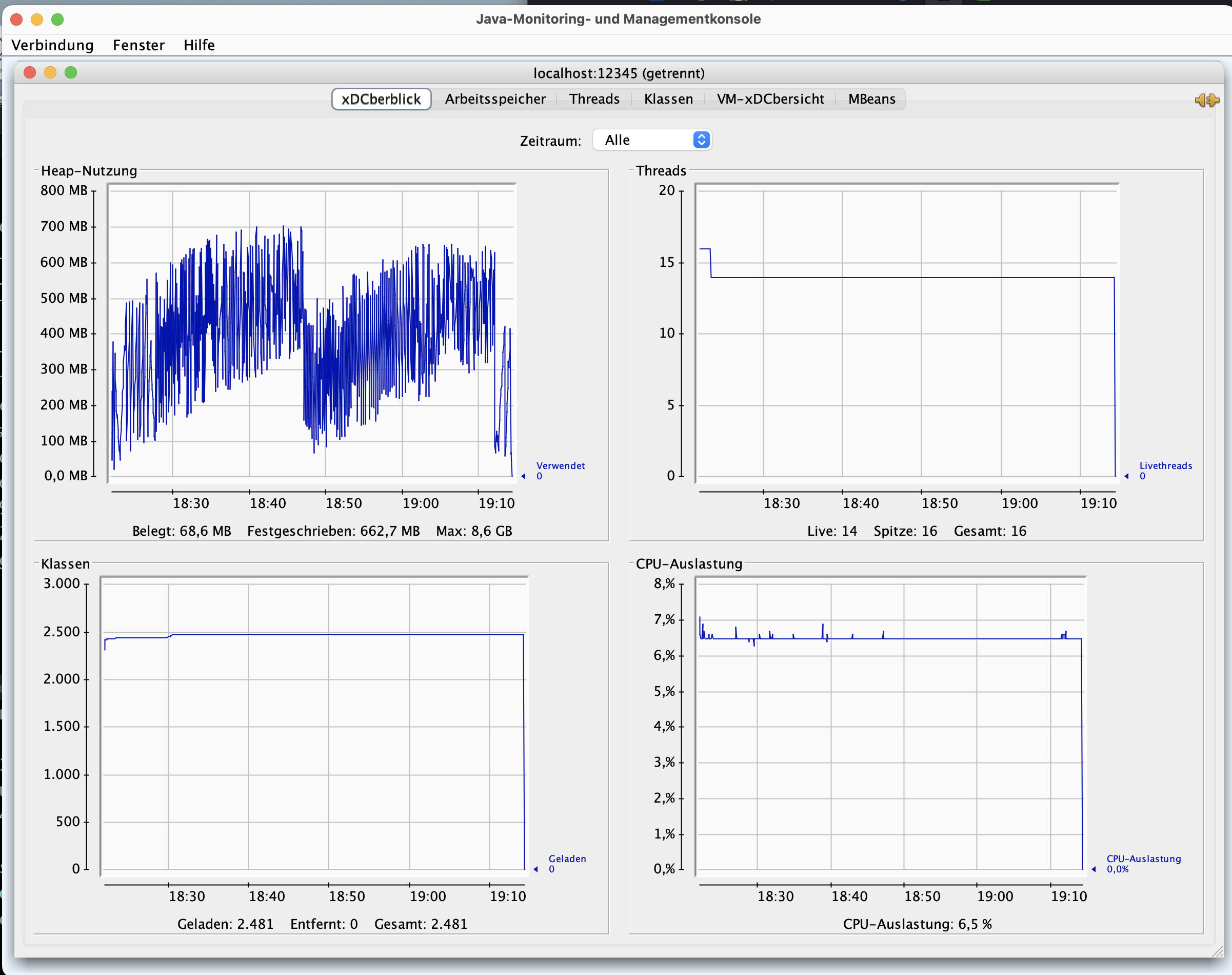
Habe es dann abgebrochen bei 32 Millionen, das Ergebnis ist auch unten in der Ausgabe-View zu sehen: