Wahrscheinlichkeitsrechnung mit dem Satz von Bayes nicht nur für Versicherungen und Medizin

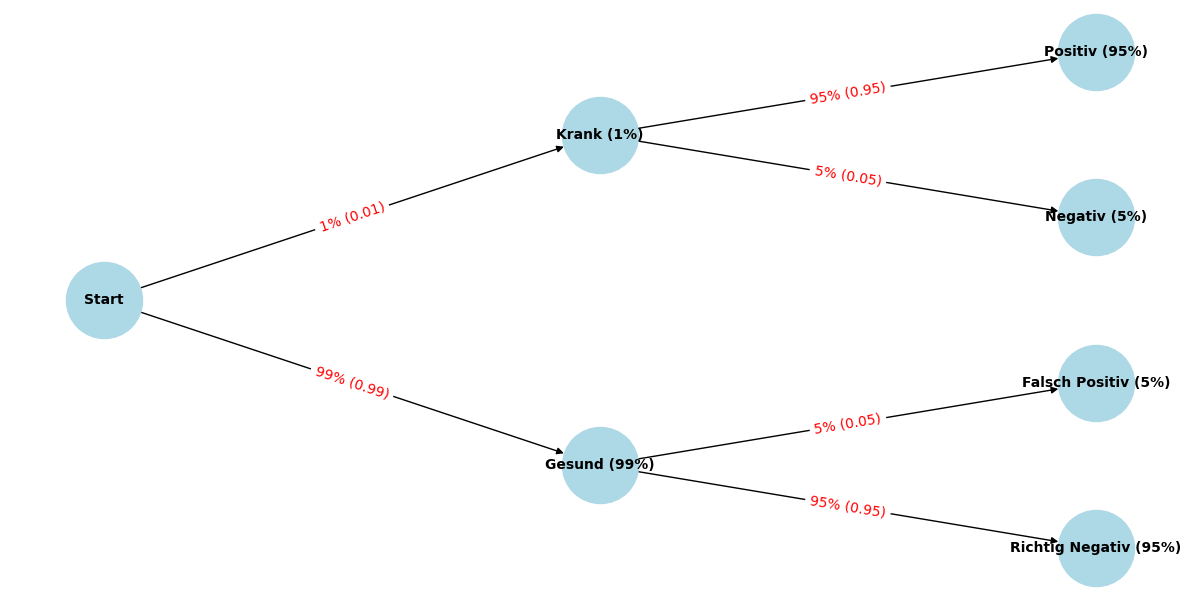
Der Satz von Bayes ist ein grundlegendes Theorem in der Wahrscheinlichkeitsrechnung, das den Zusammenhang zwischen bedingten Wahrscheinlichkeiten beschreibt.

Der Satz von Bayes ist ein spannendes Werkzeug aus der Welt der Mathematik, das uns hilft, Wahrscheinlichkeiten zu verstehen und zu berechnen. Er wird in vielen Bereichen angewendet, von der Medizin über Künstliche Intelligenz bis hin zu Alltagssituationen. Aber was genau besagt dieser Satz, und warum ist er so nützlich?

Was ist der Satz von Bayes?

Der Satz von Bayes hilft uns, eine Wahrscheinlichkeit besser einzuschätzen, wenn wir neue Informationen erhalten. Stellen Sie sich vor, Sie wollen wissen, wie wahrscheinlich es ist, dass jemand eine bestimmte Krankheit hat, wenn ein Test positiv ausfällt. Es reicht nicht aus, nur zu wissen, wie zuverlässig der Test ist – Sie müssen auch wissen, wie oft die Krankheit in der Bevölkerung vorkommt.

Der Satz von Bayes gibt uns die Formel dafür:

​

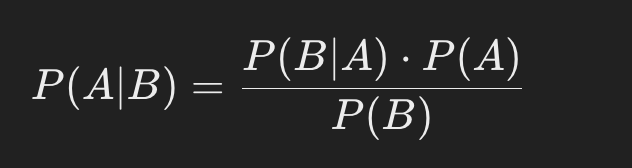
Das sieht kompliziert aus, aber keine Sorge – wir gehen es Schritt für Schritt durch und erstellen auch ein Java-Beispiel dafür.

Ein einfaches Beispiel

Stellen Sie sich vor, in einer Stadt sind 1 % der Menschen krank (Prävalenz). Es gibt einen Test, der in 95 % der Fälle eine kranke Person korrekt erkennt (Sensitivität). Aber der Test ist nicht perfekt: Bei 5 % der gesunden Menschen zeigt er fälschlicherweise ein positives Ergebnis (Falsch-Positiv-Rate).

Wenn Sie nun positiv getestet werden, wollen Sie wissen: Wie wahrscheinlich bin ich tatsächlich krank? Da hilft der Satz von Bayes.

Wir müssen drei Dinge wissen:

1. Wie häufig ist die Krankheit? Das ist P(Krank) = 0,01 oder 1 %.

2. Wie zuverlässig ist der Test bei Kranken? P(Positiv∣Krank) = 0,95 oder 95 %.

3. Wie oft gibt es ein positives Ergebnis insgesamt? Das ist P(Positiv)

Der Satz von Bayes sagt uns:

Berechnung

Die Gesamtwahrscheinlichkeit für ein positives Testergebnis (P(Positiv)) setzt sich aus zwei Teilen zusammen:

Der Test erkennt eine kranke Person als positiv: P(Positiv∣Krank)⋅P(Krank)= 0,95⋅0,01 =0,0095

Der Test zeigt fälschlicherweise positiv bei einer gesunden Person: P(Positiv∣NichtKrank)⋅P(NichtKrank)=0,05⋅0,99=0,0495

Zusammen ergibt das:

P(Positiv)=0,0095+0,0495=0,059

Jetzt setzen wir alles in die Bayes-Formel ein:

P(Krank∣Positiv) = 0,95⋅0,010,059 ≈ 0,161

Das bedeutet: Wenn Sie positiv getestet wurden, liegt die Wahrscheinlichkeit, dass Sie tatsächlich krank sind, nur bei 16 %.

Was lernen wir daraus?

Das Ergebnis mag überraschend sein, vor allem weil der Test so zuverlässig klingt. Der Grund ist, dass die Krankheit insgesamt sehr selten ist. Selbst ein guter Test erzeugt bei vielen gesunden Menschen Falsch-Positive, wenn die Krankheit selten vorkommt.

Warum ist der Satz von Bayes wichtig?

Der Satz von Bayes hilft uns, besser mit Unsicherheiten umzugehen. In der Medizin zeigt er, dass Diagnosen immer im Zusammenhang mit der Häufigkeit einer Krankheit betrachtet werden müssen.

Auch in anderen Bereichen wird er genutzt:

Künstliche Intelligenz: Um Entscheidungen basierend auf Daten zu treffen.
Versicherungen: Um Risiken zu berechnen.
Kriminalistik: Um Wahrscheinlichkeiten für bestimmte Szenarien zu bewerten.

Der Satz von Bayes ist wie ein Werkzeug, das uns zeigt, wie wir unser Wissen durch neue Informationen aktualisieren können. Egal, ob es um Medizin, Statistik oder Alltagsfragen geht – mit diesem Satz verstehen wir Wahrscheinlichkeiten besser und können klügere Entscheidungen treffen.

Jetzt noch das versprochenen Java-Programm (im git repo), aus dem Beispiel, es kann auch leicht mit anderen Werten angepasst werden:

Hier das Baumdiagramm dazu, welches ich mit Python auf dem Mac generiert habe:

Und die Vierfeldtafel um die Werte zu validieren:

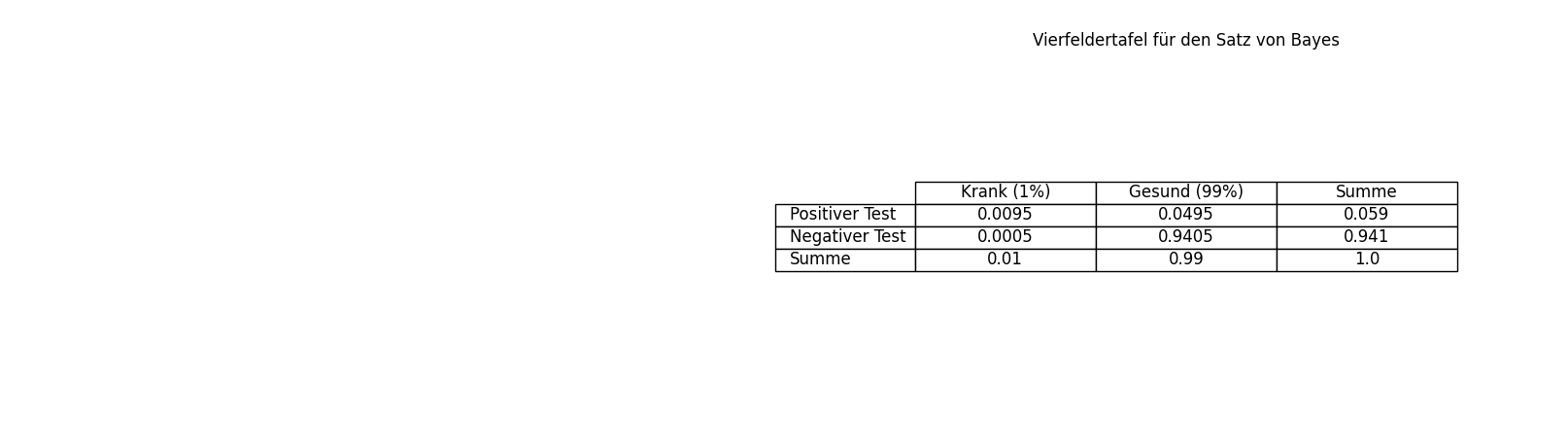
mit diesem Code:

Alles mit der coolen matplotlib.