Wir wollen mal den Erwartungswert die Varianz und die Standardabweichung bei diesen Werten 10 Euro mit 0,25 und -5 Euro mit 0,75 berechnen und mit einem Baumdiagramm darstellen. Die Berechnung soll auch in einem Java Programm mit einfacher GUI enden.

Also los, gegeben ist:
Wert X1 = 10 EuroX1 = 10Euro mit Wahrscheinlichkeit P(X1)=0,25
Wert X2 = −5 EuroX2 = −5Euro mit Wahrscheinlichkeit P(X2)=0,75

Ergebnisse:
Erwartungswert: −1,25 Euro
Varianz: 42,1875 Euro 2
Standardabweichung: 6,494 Euro
Der Erwartungswert: Gibt den durchschnittlichen Wert an, den man erwarten kann. Der gewichtete Mittelwert aller möglichen Werte, basierend auf ihren Wahrscheinlichkeiten.
Die Varianz: Misst die Streuung der Werte um den Erwartungswert. Der gewichtete Mittelwert der quadrierten Abweichungen der Werte vom Erwartungswert.
Die Standardabweichung: Zeigt die durchschnittliche Abweichung der Werte vom Erwartungswert. Die Quadratwurzel der Varianz, gibt die Streuung der Werte in derselben Einheit wie die Werte.
Mit diesem Java Programm können die Werte berechnet und dargestellt werde.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 |
package de.wenzlaff.mathe; import java.awt.BorderLayout; import java.awt.Color; import java.awt.FlowLayout; import java.awt.Graphics; import java.awt.Graphics2D; import java.awt.event.ActionEvent; import java.awt.event.ActionListener; import javax.swing.BoxLayout; import javax.swing.JButton; import javax.swing.JFrame; import javax.swing.JLabel; import javax.swing.JOptionPane; import javax.swing.JPanel; import javax.swing.JTextField; import javax.swing.SwingUtilities; /** * Berechne den Erwartungswert die Varinaz und die Standardabweichung bei diesen * Werten 10 Euro mit 0,25 und -5 Euro mit 0,75 mit kleiner GUI. * * @author Thomas Wenzlaff */ public class Standardabweichung extends JFrame { private static final long serialVersionUID = 1L; private JTextField[] valueFields = new JTextField[2]; private JTextField[] probabilityFields = new JTextField[2]; private double[] values = { 10, -5 }; private double[] probabilities = { 0.25, 0.75 }; private JPanel dataPanel; public Standardabweichung() { setTitle("Wahrscheinlichkeitsverteilung"); setSize(800, 600); setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE); setLayout(new BorderLayout()); // Eingabebereich JPanel inputPanel = createInputPanel(); add(inputPanel, BorderLayout.NORTH); // Datenvisualisierung dataPanel = new DataPanel(); add(dataPanel, BorderLayout.CENTER); } private JPanel createInputPanel() { JPanel inputPanel = new JPanel(); inputPanel.setLayout(new BoxLayout(inputPanel, BoxLayout.Y_AXIS)); // Eingabefelder für erste Wert-Wahrscheinlichkeit Kombination inputPanel.add(createLabeledField("Wert 1:", valueFields[0] = new JTextField(String.valueOf(values[0])))); inputPanel.add(createLabeledField("Wahrscheinlichkeit 1:", probabilityFields[0] = new JTextField(String.valueOf(probabilities[0])))); // Eingabefelder für zweite Wert-Wahrscheinlichkeit Kombination inputPanel.add(createLabeledField("Wert 2:", valueFields[1] = new JTextField(String.valueOf(values[1])))); inputPanel.add(createLabeledField("Wahrscheinlichkeit 2:", probabilityFields[1] = new JTextField(String.valueOf(probabilities[1])))); // Berechnungsbutton JButton calculateButton = new JButton("Berechnen"); calculateButton.addActionListener(new ActionListener() { @Override public void actionPerformed(ActionEvent e) { updateValues(); } }); inputPanel.add(calculateButton); return inputPanel; } private JPanel createLabeledField(String labelText, JTextField textField) { JPanel panel = new JPanel(new FlowLayout(FlowLayout.LEFT)); panel.add(new JLabel(labelText)); panel.add(textField); textField.setColumns(10); return panel; } private void updateValues() { try { // Werte aus Eingabefeldern auslesen values[0] = Double.parseDouble(valueFields[0].getText()); values[1] = Double.parseDouble(valueFields[1].getText()); probabilities[0] = Double.parseDouble(probabilityFields[0].getText()); probabilities[1] = Double.parseDouble(probabilityFields[1].getText()); // Neuzeichnen des Panels dataPanel.repaint(); } catch (NumberFormatException ex) { JOptionPane.showMessageDialog(this, "Bitte gültige Zahlen eingeben!"); } } private class DataPanel extends JPanel { @Override protected void paintComponent(Graphics g) { super.paintComponent(g); Graphics2D g2d = (Graphics2D) g; // Hintergrund g2d.setColor(Color.WHITE); g2d.fillRect(0, 0, getWidth(), getHeight()); // Balkendiagramm int startX = 100; int startY = 300; int barWidth = 100; int maxHeight = 200; for (int i = 0; i < values.length; i++) { double scaledHeight = Math.abs(values[i]) * (maxHeight / 10.0); g2d.setColor(values[i] >= 0 ? Color.GREEN : Color.RED); g2d.fillRect(startX + i * 150, startY - (int) scaledHeight, barWidth, (int) scaledHeight); g2d.setColor(Color.BLACK); g2d.drawString(String.format("Wert %d", i + 1), startX + i * 150, startY + 30); g2d.drawString(String.format("%.2f€ (%.2f%%)", values[i], probabilities[i] * 100), startX + i * 150, startY + 50); } // Statistische Berechnungen double expectation = calculateExpectation(); double variance = calculateVariance(expectation); double stdDeviation = Math.sqrt(variance); g2d.drawString(String.format("Erwartungswert: %.2f€", expectation), 50, 50); g2d.drawString(String.format("Varianz: %.2f", variance), 50, 70); g2d.drawString(String.format("Standardabweichung: %.2f€", stdDeviation), 50, 90); } private double calculateExpectation() { double sum = 0; for (int i = 0; i < values.length; i++) { sum += values[i] * probabilities[i]; } return sum; } private double calculateVariance(double expectation) { double variance = 0; for (int i = 0; i < values.length; i++) { variance += Math.pow(values[i] - expectation, 2) * probabilities[i]; } return variance; } } public static void main(String[] args) { SwingUtilities.invokeLater(() -> { new Standardabweichung().setVisible(true); }); } } |
Es kann auch hier auf Gitlab geladen werden.
Bekommen wir dieses Ergebnis:
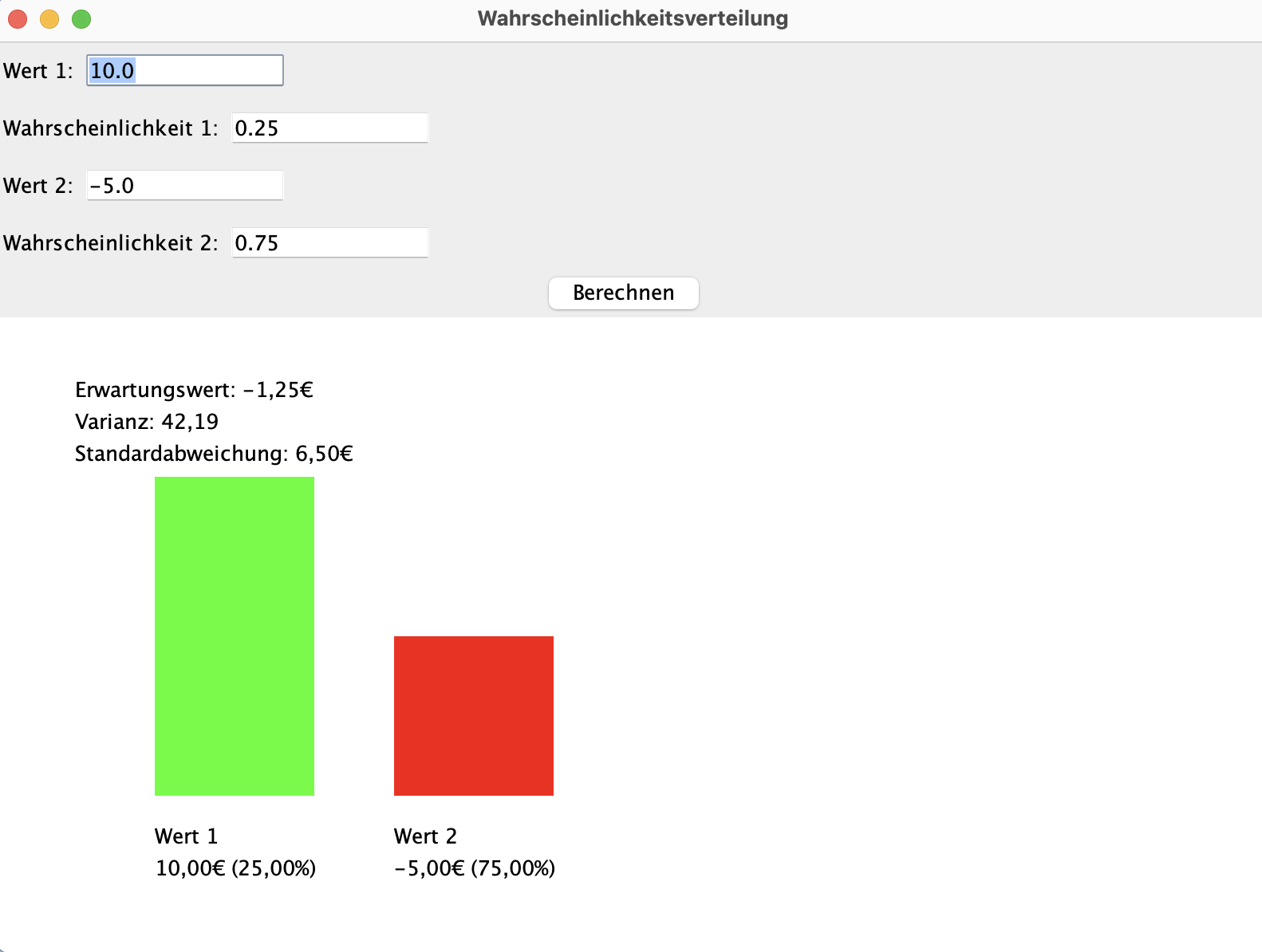
Dann noch eben ein Baumdiagramm für das Beispiel:
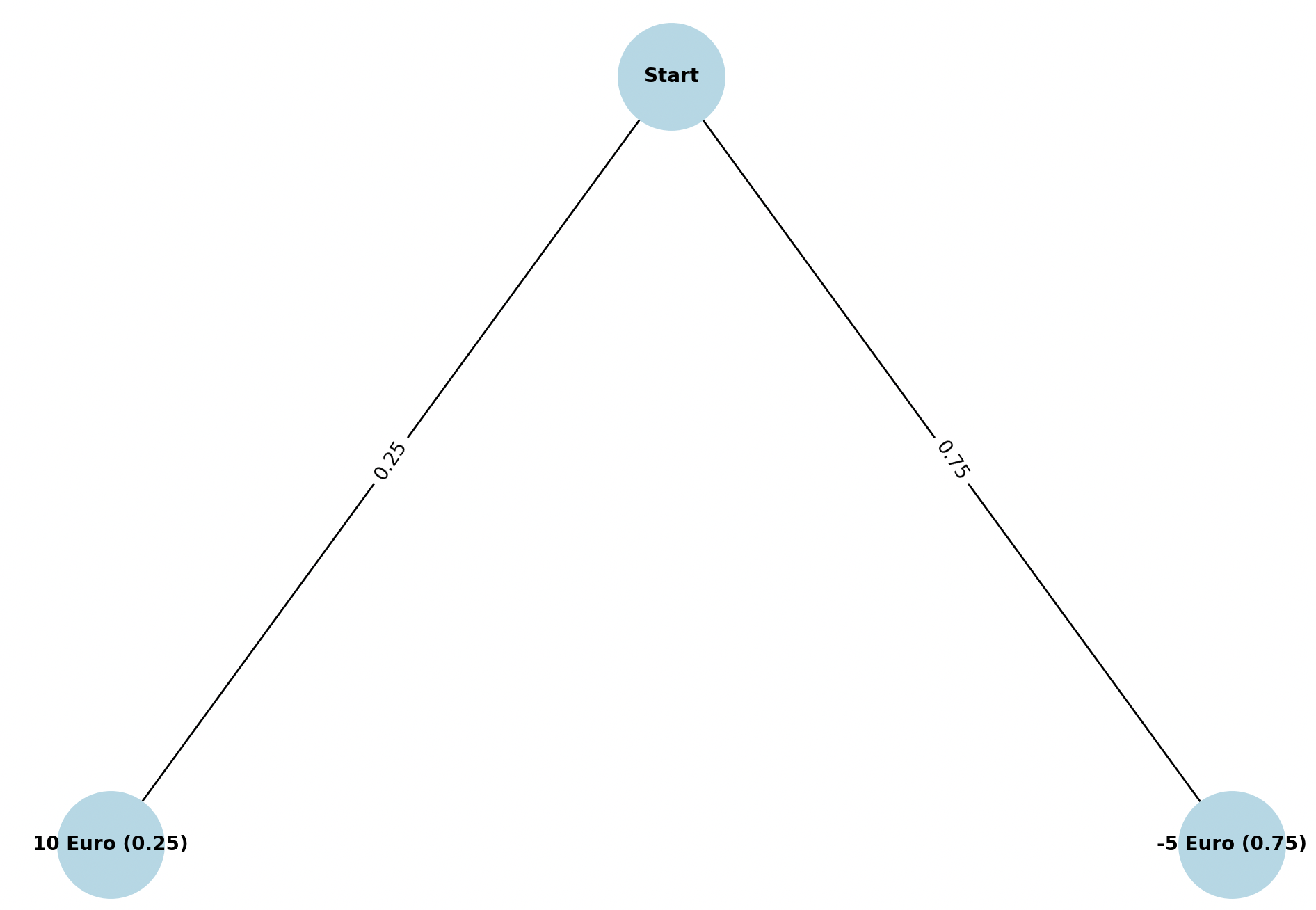
Hier der Python Code dazu:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
#!/usr/bin/env python # Thomas Wenzlaff, kleinhirn.eu import matplotlib.pyplot as plt import networkx as nx import matplotlib.pyplot as plt import networkx as nx # Daten für das Baumdiagramm edges = [ ("Start", "10 Euro (0.25)"), ("Start", "-5 Euro (0.75)"), ] # Graphen initialisieren G = nx.DiGraph() G.add_edges_from(edges) # Positionen der Knoten für Layout pos = { "Start": (0, 1), "10 Euro (0.25)": (-1, 0), "-5 Euro (0.75)": (1, 0), } # Plot erstellen plt.figure(figsize=(8, 6)) nx.draw(G, pos, with_labels=True, node_size=3000, node_color="lightblue", font_size=10, font_weight="bold", arrows=False) # Wahrscheinlichkeiten hinzufügen nx.draw_networkx_edge_labels( G, pos, edge_labels={ ("Start", "10 Euro (0.25)"): "0.25", ("Start", "-5 Euro (0.75)"): "0.75", }, font_size=10 ) # Diagramm anzeigen plt.title("Baumdiagramm für Erwartungswert, Varianz und Standardabweichung", fontsize=12) plt.axis("off") plt.show() |
