Der Interquartilsabstand (IQR) ist ein Streuungsmaß in der deskriptiven Statistik. Der IQR ist eine robuste Maßzahl, die in der Lage ist, Ausreißer in Datensätzen zu identifizieren und Informationen über die Streuung der Daten zu liefern. Der Interquartilsabstand, oft abgekürzt als IQR, ist ein Maß für die Streuung oder die Verbreitung von Daten in einem Datensatz. Er basiert auf den Quartilen, die die Daten in vier gleich große Teile aufteilen.

Die Quartile sind:
Q1 (erstes Quartil): Der Wert, unterhalb dessen sich das untere Viertel der Daten befindet. Dies entspricht dem 25. Perzentil der Daten.
Q2 (zweites Quartil): Der Median oder der Wert, der das mittlere Viertel der Daten teilt. Dies entspricht dem 50. Perzentil der Daten und ist der Median des Datensatzes.
Q3 (drittes Quartil): Der Wert, unterhalb dessen sich das obere Viertel der Daten befindet. Dies entspricht dem 75. Perzentil der Daten.
Der Interquartilsabstand wird berechnet, indem man den Unterschied zwischen dem dritten Quartil (Q3) und dem ersten Quartil (Q1) subtrahiert:
IQR=Q3−Q1
Der IQR ist ein nützliches Werkzeug für die Datenanalyse aus mehreren Gründen:
Robuste Maßzahl: Im Gegensatz zu anderen Maßzahlen, wie dem Durchschnitt oder der Standardabweichung, ist der IQR robust gegenüber Ausreißern in den Daten. Dies bedeutet, dass extreme Werte in einem Datensatz den IQR weniger beeinflussen als andere Maßzahlen.
Identifizierung von Ausreißern: Der IQR wird oft verwendet, um Ausreißer zu identifizieren. Datenpunkte, die unterhalb von Q1−1,5×IQRQ1−1,5×IQR oder oberhalb von Q3+1,5×IQRQ3+1,5×IQR liegen, werden als potenzielle Ausreißer betrachtet.
Streuung und Variabilität: Der IQR gibt Informationen über die Streuung oder die Variabilität der Daten. Ein großer IQR deutet auf eine größere Variabilität hin, während ein kleiner IQR auf eine geringere Variabilität hinweist.
Boxplots: Der IQR ist ein zentraler Bestandteil von Boxplots, die visuell die Verteilung der Daten und Ausreißer darstellen. Der IQR definiert die Länge des Kastens in einem Boxplot.
Kommen wir nun zu einem Beispiel mit PSPP. Wir nehmen wieder den Datensatz der Blutransfusionen.
Im Menü: Analysieren – Deskriptive Statistiken – Explorative Datenanalyse können wir den Interquartilsabstand berechnen lassen, dazu diese Optionen auswählen:
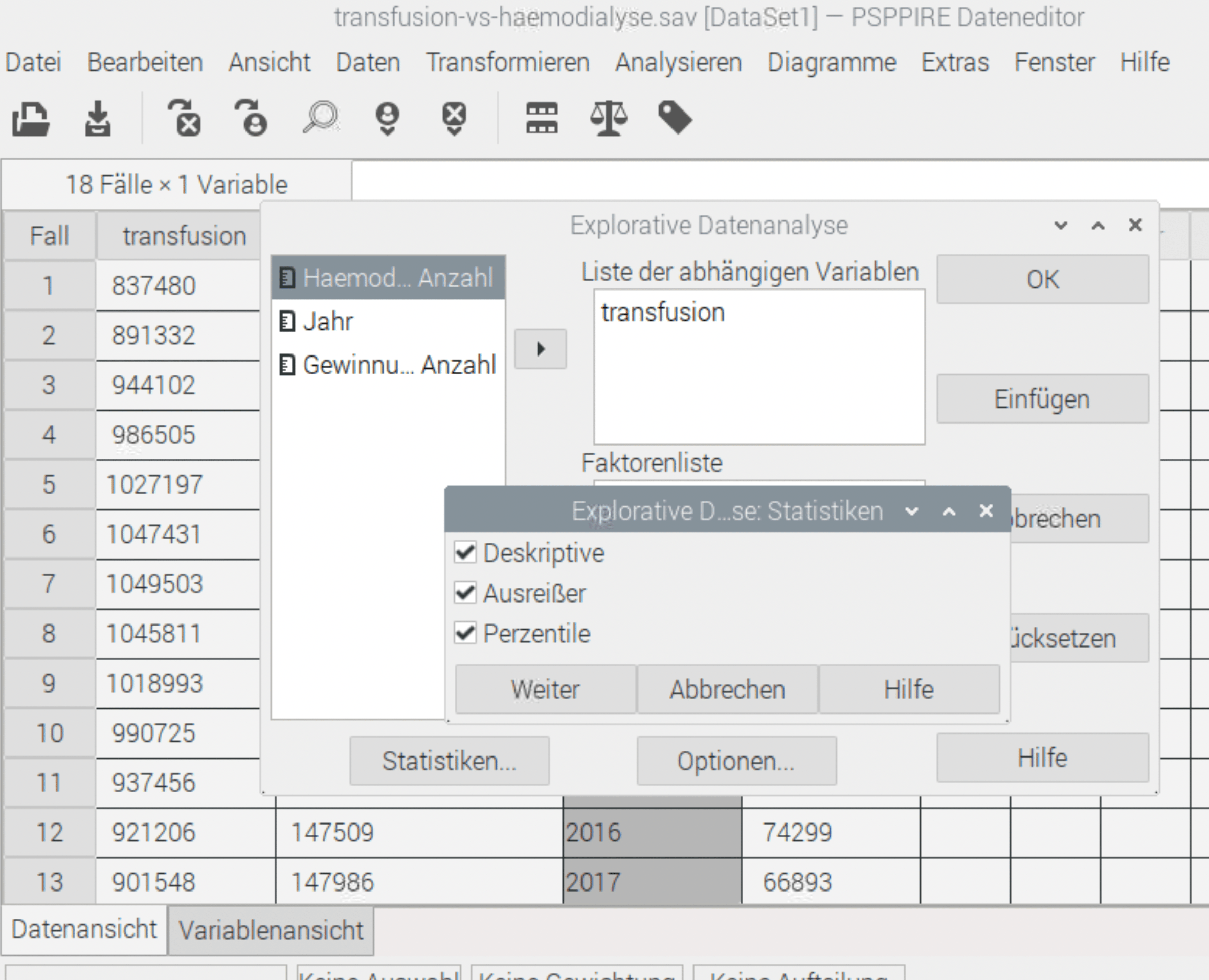
Und wir erhalten das Ergebnis:
|
1 2 3 4 5 |
Examine variables=transfusion /statistics descriptives /missing listwise /nototal / PERCENTILE= ROUND |
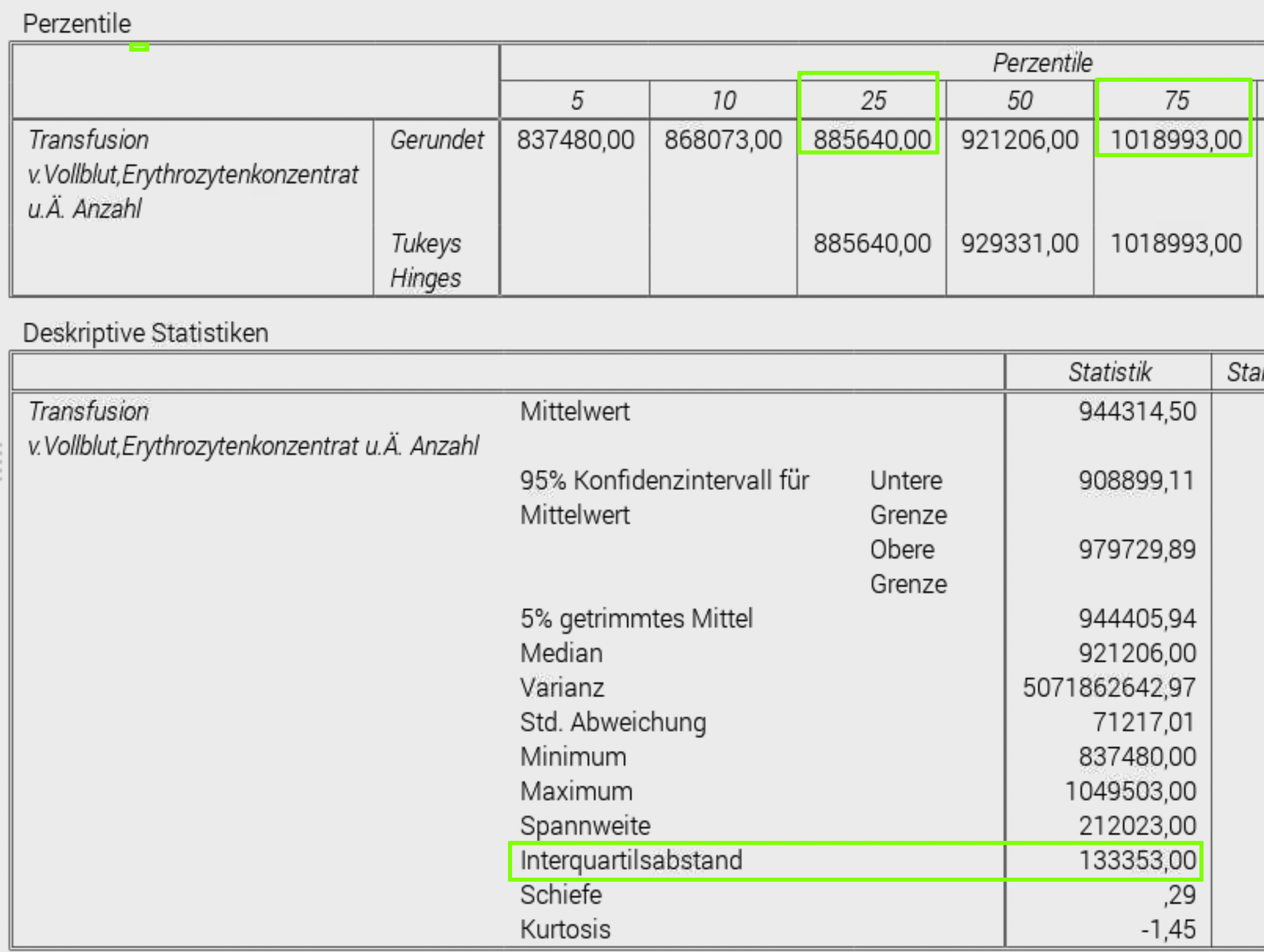
Wenn wir das per Hand nachrechnen:
3. Quartil = 1018993 – 1. Quartil = 885640 = 133353
Oder per Excel:
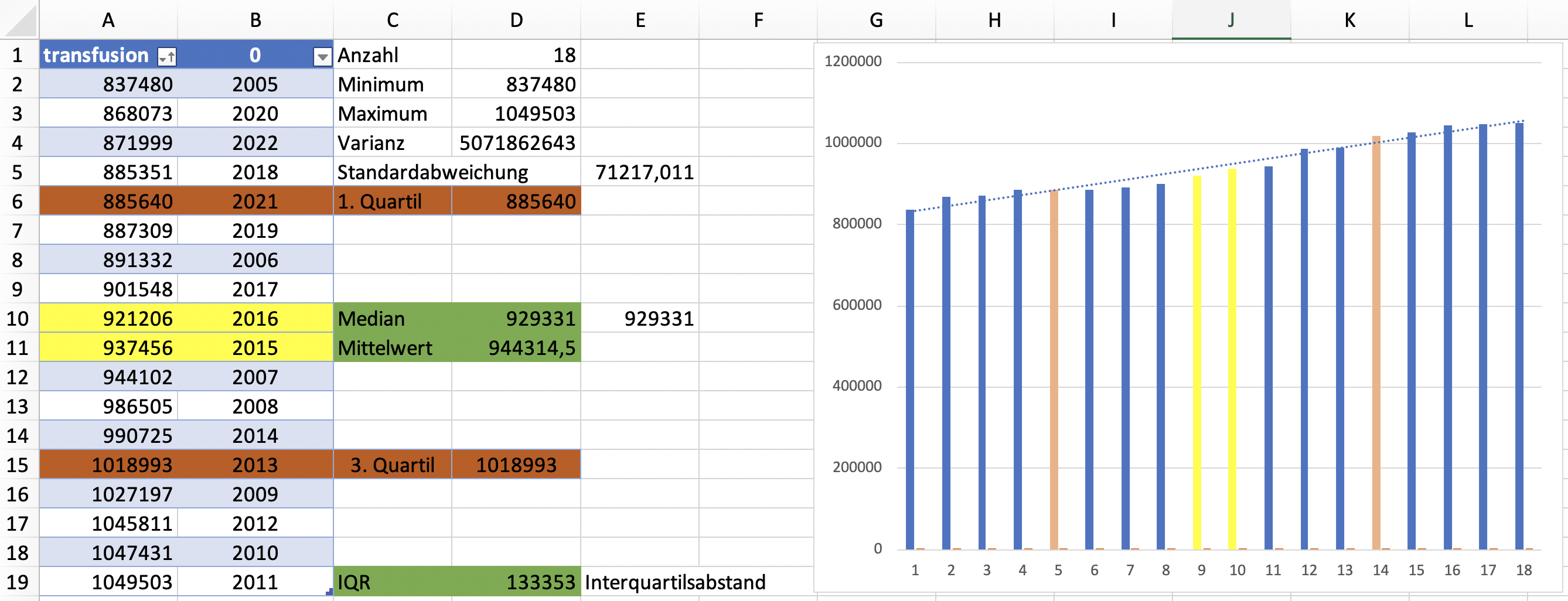
Oder wenn wir es im Online-Rechner berechnen lassen:

„Interquartilsabstand-Rechner“ at https://miniwebtool.com/de/interquartile-range-calculator/ from miniwebtool, https://miniwebtool.com/
Ok, validiert.
Es gibt unterschiedliche Formeln für die Berechnung des IQR in PSPP, wir haben hier den gerundeten Durchschnit ( ROUND ) verwendet, als Optionen gibt es noch diese:
/PERCENTILE=[percentiles]={HAVERAGE, WAVERAGE, ROUND, AEMPIRICAL, EMPIRICAL }
Die Hauptunterschiede zwischen diesen Konzepten liegen in ihren Anwendungen und Berechnungsmethoden. Die Wahl des richtigen Durchschnitts oder Streuungsmaßes hängt von den spezifischen Anforderungen Ihrer Analyse und den Eigenschaften Ihrer Daten ab. Es ist wichtig, das geeignete Maß für Ihre spezielle Fragestellung und Ihre Daten auszuwählen. Hier sind kurz die wichtigsten Unterschiede zwischen diesen Konzepten:
HAVERAGE (Harmonic Mean):
Die harmonische Mittelwert ist das Kehrwert des Durchschnitts der Kehrwerte der Daten. Es wird oft verwendet, wenn Sie den Durchschnitt von Werten berechnen möchten, die in einer Weise miteinander verknüpft sind, bei der die harmonische Mittelwert eine bessere Darstellung liefert als der arithmetische Mittelwert. Die Berechnungsformel ist: N / (1/x1 + 1/x2 + … + 1/xN), wobei N die Anzahl der Datenpunkte und x1, x2, …, xN die Datenwerte sind.
WAVERAGE (Weighted Average):
Der gewichtete Durchschnitt berücksichtigt, dass einige Datenpunkte stärker gewichtet werden als andere. Es wird verwendet, wenn Sie den Durchschnitt von Werten berechnen möchten, wobei einige Datenpunkte mehr Einfluss auf das Ergebnis haben. Die Berechnungsformel ist: (w1 * x1 + w2 * x2 + … + wN * xN) / (w1 + w2 + … + wN), wobei w1, w2, …, wN die Gewichtungen der Datenpunkte sind.
ROUND (Gerundeter Durchschnitt):
Runden Sie alle Datenwerte auf die gleiche Anzahl von Dezimalstellen. Berechnen Sie den arithmetischen Durchschnitt der gerundeten Werte. Die gerundete Methode wird verwendet, um Daten zu vereinfachen, insbesondere wenn die Originaldaten sehr präzise sind.
AEMPIRICAL (Angepasster empirischer IQR):
AEMPIRICAL ist eine Methode zur Berechnung des Interquartilsabstands (IQR), die Datenpunkte in einem Datensatz verwendet, um den Wert des IQR zu schätzen.Es verwendet die Formel AEMPIRICAL IQR = 0.7413 * (X(Q3) – X(Q1)), wobei X(Q3) und X(Q1) die Werte des dritten und ersten Quartils sind.
EMPIRICAL IQR (Empirischer Interquartilsabstand):
Der empirische Interquartilsabstand ist ein Maß für die Streuung, das auf den empirischen Datenpunkten basiert. Es verwendet den IQR von tatsächlichen Datenpunkten, um die Streuung der Daten zu quantifizieren.
Der Interquartilsabstand ist ein leistungsstarkes Werkzeug in der statistischen Analyse. Er liefert Informationen über die Streuung von Daten, identifiziert Ausreißer und ermöglicht die Visualisierung von Daten mithilfe von Boxplots. Aufgrund seiner Robustheit und seiner Fähigkeit, die Verteilung von Daten zu beschreiben, ist der IQR ein unverzichtbares Instrument in der Statistik. Bei der Analyse von Daten sollte der IQR in Verbindung mit anderen statistischen Maßzahlen und Visualisierungen verwendet werden, um ein umfassendes Verständnis der Daten zu gewährleisten.
