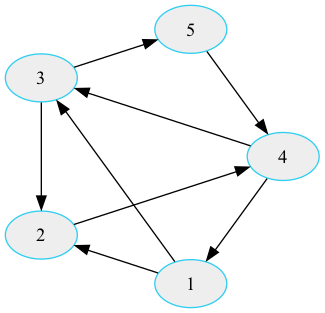
Das „Haus vom Nikolaus“ mit seinen 88 Möglichkeiten und seine Bedeutung in der Graphentheorie

Das „Haus vom Nikolaus„, ein einfaches geometrisches Muster aus fünf Linien, das die Form eines stilisierten Hauses darstellt, mag auf den ersten Blick wie eine unschuldige Kindermalerei wirken. Doch hinter diesem scheinbar simplen Muster verbirgt sich eine faszinierende Verbindung zur Graphentheorie, einem Teilgebiet der Mathematik, das sich mit den Eigenschaften und Beziehungen von Graphen beschäftigt. Dann mal los, und ein kleines Java Programm dazu.

Was ist das „Haus vom Nikolaus“?

Das „Haus vom Nikolaus“ ist eine Zeichnung, die aus fünf Strichen besteht und die Form eines stilisierten Hauses zeigt. Es besteht aus einem Quadrat als Basis, einem Dreieck als Dach und einem rechteckigen Schornstein oben auf dem Dach. Es ist benannt nach dem „Nikolaus, dem Schutzpatron der Kinder“, da es oft von Kindern gezeichnet wird.

Graphentheorie und das „Haus vom Nikolaus“

Die Verbindung zwischen dem „Haus vom Nikolaus“ und der Graphentheorie liegt in der Möglichkeit, die Zeichnung als Graphen darzustellen. Ein Graph in der Mathematik besteht aus Knoten (auch als Ecken oder Punkte bezeichnet) und Kanten (auch als Linien oder Verbindungen bezeichnet), die die Beziehungen zwischen den Knoten repräsentieren. In diesem Zusammenhang können die Ecken des „Hauses vom Nikolaus“ als Knoten betrachtet werden, während die Linien zwischen den Ecken die Kanten darstellen. Wie oben oder hier als gerichteter Graph:

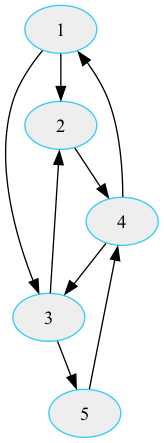
Die Bedeutung der „Haus vom Nikolaus“-Graphen

Der „Haus vom Nikolaus“-Graph ist ein Beispiel für einen nicht-planaren Graphen. Ein planarer Graph ist ein Graph, der so auf einer Ebene gezeichnet werden kann, dass sich keine seiner Kanten überschneiden. Der „Haus vom Nikolaus“-Graph kann jedoch nicht ohne Kantenüberschneidungen auf eine Ebene gezeichnet werden, was ihn zu einem klassischen Beispiel für einen nicht-planaren Graphen macht.

Ein Graph G ist ein Tupel (V,E), wobei V eine Menge von Knoten (englisch vertex, oft auch Ecken genannt) und E eine Menge von Kanten (engl. edge, manchmal auch Bögen genannt) bezeichnet.

In der Graphentheorie gibt es den berühmten Satz von dem polnischen Mathematiker Kuratowski, der besagt, dass ein Graph genau dann nicht-planar ist, wenn er einen Teilgraphen enthält, der homomorph zu einem „Haus vom Nikolaus“-Graphen ist. Das bedeutet, dass das „Haus vom Nikolaus“ eine wichtige Rolle in der Untersuchung von nicht-planaren Graphen spielt und als Beispiel dient, um verschiedene Konzepte und Eigenschaften von Graphen zu veranschaulichen.

Das „Haus vom Nikolaus“ mag auf den ersten Blick wie eine einfache Kindermalerei aussehen, aber es hat eine tiefere Bedeutung in der Welt der Graphentheorie. Es veranschaulicht die Idee von nicht-planaren Graphen und bietet ein anschauliches Beispiel für den berühmten Satz von Kuratowski. Dieses scheinbar unschuldige Muster ist ein hervorragendes Beispiel dafür, wie abstrakte mathematische Konzepte in visuellen Darstellungen veranschaulicht werden können, um komplexe Ideen zu vermitteln.

Dann mal hier ein Beispiel in Java und mit jGrapht:

Und eine Testklasse dazu:

Wer noch ein Template für Graphviz braucht:

Nun fehlt noch ein kleines Programm, um alle 88 Möglichkeiten zu erzeugen. Der ganze Quellcode ist auf GitLab. Aber nicht mehr heute …