Das Königsberger Brückenproblem ist eine klassische mathematische Herausforderung, die im 18. Jahrhundert entstand und einen wichtigen Einfluss auf die Entwicklung der Graphentheorie hatte. Es handelt sich um eine Fragestellung bezüglich der Überquerung von Brücken über den Flüssen Pregel und seinen Inseln in der Stadt Königsberg (heute Kaliningrad, Russland). Das Problem wurde erstmals von dem Schweizer Mathematiker Leonhard Euler im Jahr 1735 gelöst und legte den Grundstein für die moderne Graphentheorie.
In Königsberg gab es sieben Brücken, die die Flüsse Pregel und die beiden Inseln verbunden haben. Die Frage war, ob es möglich war, die Stadt zu durchqueren, indem man jede Brücke nur einmal überquerte und schließlich an einem beliebigen Punkt endete.
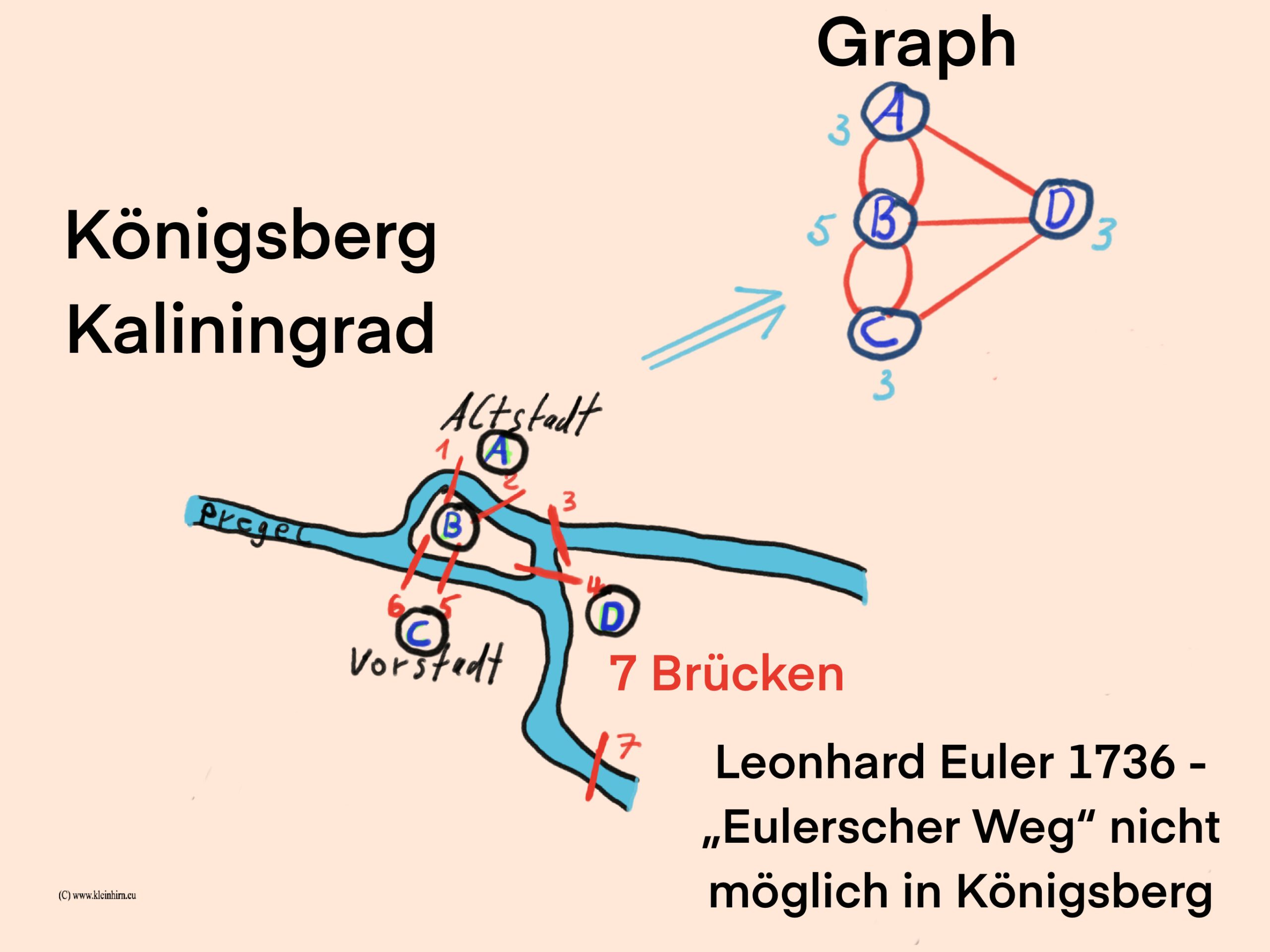
Euler bewies, dass es keine Möglichkeit gibt, das Königsberger Brückenproblem zu lösen. Er zeigte, dass mindestens zwei der vier Landpunkte eine ungerade Anzahl von Brücken haben müssten, um eine Lösung unmöglich zu machen. Dies führte zur Entwicklung der Graphentheorie, bei der das Problem als ein Graph dargestellt werden kann, wobei die Landpunkte die Knoten und die Brücken die Kanten des Graphen sind.
Da kommt nun die Implementierung mit JGraphT in Java ins Spiel.
JGraphT ist eine Java-Bibliothek, die es ermöglicht, Graphen einfach zu erstellen, zu manipulieren und zu analysieren.
Hier ist ein Beispiel, wie das Königsberger Brückenproblem mit JGraphT in Java implementiert werden kann.
Zuerst müssen Sie die JGraphT-Bibliothek zu Ihrem Projekt hinzufügen. Dies kann normalerweise durch das Hinzufügen einer Abhängigkeit in Ihrer Build-Datei (z.B. Maven pom.xml) erfolgen.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
<dependency> <groupId>org.jgrapht</groupId> <artifactId>jgrapht-core</artifactId> <version>1.5.2</version> </dependency> <dependency> <groupId>org.jgrapht</groupId> <artifactId>jgrapht-ext</artifactId> <version>1.5.2</version> </dependency> <dependency> <groupId>com.github.vlsi.mxgraph</groupId> <artifactId>jgraphx</artifactId> <version>4.2.2</version> </dependency> <dependency> <groupId>org.jgrapht</groupId> <artifactId>jgrapht-io</artifactId> <version>1.5.2</version> </dependency> |
Dann können wir in Java den ungerichteten Graphen mit der Multigraph Klasse erzeugen:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
// Erstelle einen ungerichteten Graphen mit Multiple edges graph = new DefaultListenableGraph<>(new Multigraph<>(DefaultEdge.class)); // Füge 4 Knoten (Landpunkte) zum Graphen hinzu graph.addVertex("A"); graph.addVertex("B"); graph.addVertex("C"); graph.addVertex("D"); // Füge 7 Kanten (Brücken) zwischen den Knoten hinzu graph.addEdge("A", "B"); graph.addEdge("A", "B"); graph.addEdge("A", "D"); graph.addEdge("B", "D"); graph.addEdge("B", "C"); graph.addEdge("B", "C"); graph.addEdge("C", "D"); |
Wir können auch eine dot Datei erzeugen:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
graph G { 1 [ label="A" style="filled" fillcolor="#EEEEEE" color="#31CEF0" ]; 2 [ label="B" style="filled" fillcolor="#EEEEEE" color="#31CEF0" ]; 3 [ label="C" style="filled" fillcolor="#EEEEEE" color="#31CEF0" ]; 4 [ label="D" style="filled" fillcolor="#EEEEEE" color="#31CEF0" ]; 1 -- 2; 1 -- 2; 1 -- 4; 2 -- 4; 2 -- 3; 2 -- 3; 3 -- 4; } |
Die kann dann leicht mit
dot -T png -o koenigsberger-dot.png $inputDateiname
in diese Grafik übersetzt werden.
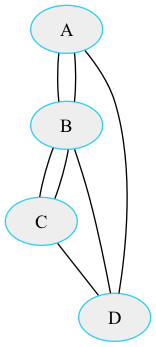
Die Frage war, ob es einen Weg gibt, bei dem man alle sieben Brücken genau einmal überquert, und wenn ja, ob auch ein Rundweg möglich ist, bei dem man wieder zum Ausgangspunkt gelangt. Leonhard Euler bewies 1736, dass ein solcher Weg bzw. Eulerscher Weg in Königsberg nicht möglich war, da zu allen vier Ufergebieten bzw. Inseln eine ungerade Zahl von Brücken führte. Es dürfte maximal zwei Ufer (Knoten) mit einer ungeraden Zahl von angeschlossenen Brücken (Kanten) geben. Diese zweiUfer könnten Ausgangs- bzw. Endpunkt sein. Die restlichen Ufer müssten eine gerade Anzahl von Brücken haben, um sie auch wieder auf einem neuen Weg verlassen zu können.
Durch Kriegseinwirkung und Umbauten nach 1945 ist die ursprüngliche Situation im heutigen Kaliningrad nicht mehr gegeben. Zwei der zur Insel Kneiphof führenden Brücken existieren nicht mehr; am nördlichen und südlichen Ufer enden nur noch jeweils zwei anstatt drei Brücken. Nun ist zwar ein Eulerweg möglich, jedoch noch immer kein Eulerkreis.
Zum überprüfen des Graph ob er einen „Eulerschen Weg“ ermöglicht, kann die die HierholzerEulerianCycle Klasse wie folgt aufgerufen werden.
|
1 2 |
HierholzerEulerianCycle<Object, DefaultEdge> hier = new HierholzerEulerianCycle<>(); boolean isEulerian = hier.isEulerian(graph); |
Hier gibt es auch eine schöne Online-Seite dazu.
Das Königsberger Brückenproblem hat nicht nur die Graphentheorie beeinflusst, sondern auch dazu beigetragen, die Grundlagen für das Verständnis von Netzwerken und Verbindungen zu legen. Durch die Verwendung von JGraphT und anderen modernen Technologien können wir diese historische mathematische Herausforderung mühelos in Java implementieren und verstehen, wie graphentheoretische Konzepte auf reale Probleme angewendet werden können.
Das ganze Projekt und auch die JUnit-Test kann von hier geclont werden. Auch gibt es dort noch einige Bilder zu dem Thema bzw. Scripte.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
In Königsberg, Stadt am Fluss so klar, Das Brückenproblem war wahrlich rar. Sieben Brücken führten über's Wasser blau, Die Frage war: "Wie kommt man auf die andere Au?" Leonhard Euler kam, mit Geist so wach, Er dachte nach, und ohne Zwang und Drach'. Graphentheorie, sein Werk so klug, Löste das Rätsel, mit einem einzigen Zug. Vier Landpunkte standen, A, B, C und D, Kanten und Knoten, ein kniffliges Gedicht. Die Brücken verbanden, mit List und Verstand, Doch eine Route fand sich nicht im Land. Die Graphen halfen, das Rätsel zu lösen, Mit Algorithmen und Wissen, so groß. Eulerkreis und Konnektivität, Die Mathematik brachte Klarheit herbei. So bleibt das Rätsel, in Erinnerung stets, Wie Euler's Köpfchen das Problem erfasst. Die sieben Brücken, ein Denkspiel für die Zeit, Graphentheorie, im Mittelalter geweiht. -Thomas Wenzlaff |
Hier noch der Graph, von dem ganzen Projekt:
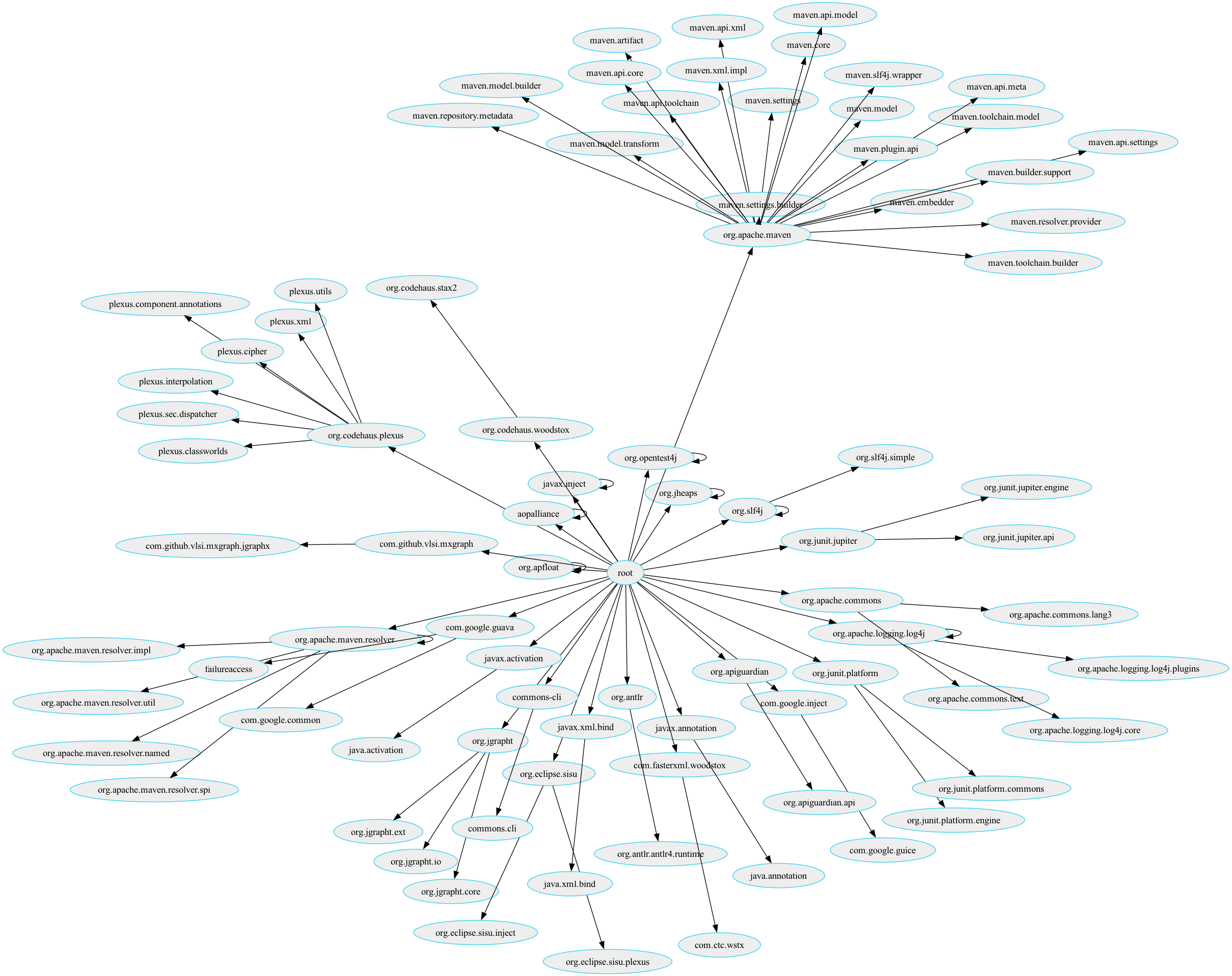oder wer es als Video sehen will.