Sierpinski-Dreieck: Mal was anderes als der Mega-Hack der Bybit Exchange mit ca. 401000 ETH ( ca. 1,4 Milliarden Dollar ) Verlust – Wenzlaff.de

Der Crypto-Bereich ist in Aufregung, weil Bybit von einem Ethereum-Cold-Wallet ca. 1,4 Milliarden Dollar geklaut wurden. Wie war das technisch möglich? Hier eine Erklärungsmöglichkeit:

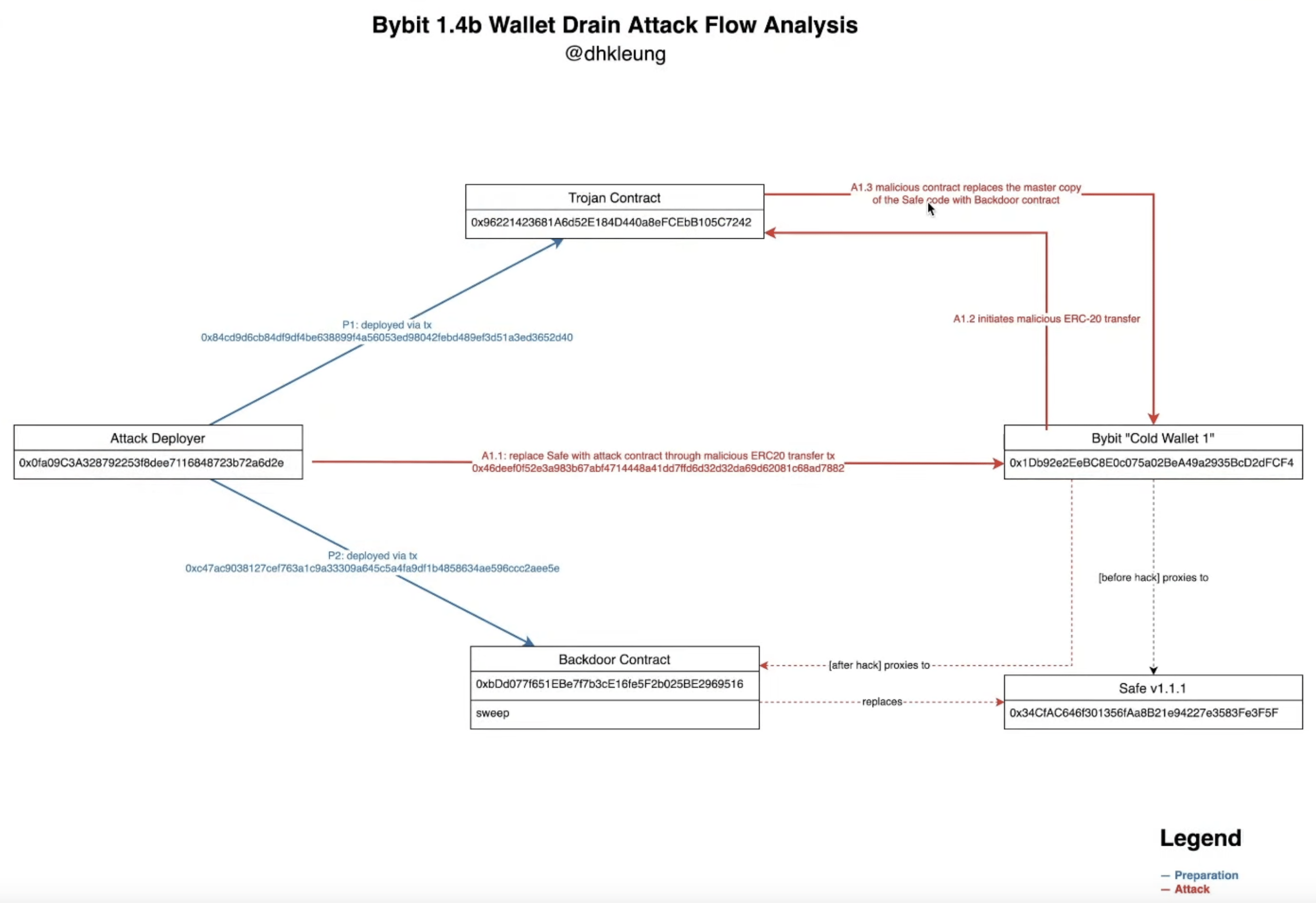
Aber kommen wir nun zu etwas einfacheren und auch sehr interessanten Thema: Das Sierpinski-Dreieck. Das Sierpinski-Dreieck ist ein faszinierendes mathematisches Konstrukt, das als selbstähnlicher Fraktal bekannt ist.

Obwohl das Sierpinski-Dreieck nach dem polnischen Mathematiker Wacław Sierpiński benannt ist, der es 1915 formal beschrieb, gibt es Hinweise darauf, dass ähnliche Muster bereits in der mittelalterlichen Kunst und Architektur verwendet wurden. Beispielsweise wurden solche Muster in den Cosmati-Mosaiken in römischen Kirchen des 13. Jahrhunderts gefunden.

Das Sierpinski-Dreieck wird durch eine rekursive Methode erzeugt, bei der man mit einem gleichseitigen Dreieck beginnt und dann wiederholt kleinere gleichseitige Dreiecke innerhalb des größeren Dreiecks entfernt. Der Prozess ist wie folgt:

– Beginne mit einem gleichseitigen Dreieck.
– Verbinde die Mittelpunkte der Seiten, um vier kleinere gleichseitige Dreiecke zu erzeugen.
– Entferne das mittlere Dreieck, sodass nur drei kleinere Dreiecke übrig bleiben.
– Wiederhole diesen Prozess unendlich oft mit den verbleibenden Dreiecken.

Das Sierpinski-Dreieck ist nicht nur ein theoretisches Konstrukt, sondern hat auch praktische Anwendungen in der Kunst, Technologie und Wissenschaft. Seine selbstähnliche Struktur und die unendliche Wiederholung machen es zu einem faszinierenden Objekt der Mathematik und der Fraktalgeometrie.

Fraktal-generierende Software: Das Sierpinski-Dreieck dient als Grundlage für Software, die Fraktale erzeugt, und wird in der Spezialeffekte-Industrie für Filme verwendet. In Java kann man so ein Programm leicht erstellen, es werden die Bilder wie oben in einen einfachen Swing Rahmen angezeigt:

import java.awt.Dimension;
import java.awt.Graphics;
import java.awt.Point;

import javax.swing.JFrame;
import javax.swing.JPanel;
import javax.swing.Timer;

/**
 * Sierpinski Dreieck.
 * https://de.wikipedia.org/wiki/Fraktal
 * https://de.wikipedia.org/wiki/Sierpinski-Dreieck
 * 
 * @author Thomas Wenzlaff
 *
 */
public class SierpinskiTriangle extends JPanel {

	private static final int VERZOEGERUNG_IN_SEKUNDEN = 2000;

	private static final long serialVersionUID = 1L;

	private int order = 1;
	private Timer timer;

	public SierpinskiTriangle() {
		setPreferredSize(new Dimension(1200, 1200));

		timer = new Timer(VERZOEGERUNG_IN_SEKUNDEN, e -> {
			order = (order % 10) + 1;
			repaint();
		});
		timer.start();
	}

	@Override
	protected void paintComponent(Graphics g) {
		super.paintComponent(g);
		Point p1 = new Point(getWidth() / 2, 10);
		Point p2 = new Point(10, getHeight() - 10);
		Point p3 = new Point(getWidth() - 10, getHeight() - 10);
		displayTriangles(g, order, p1, p2, p3);
	}

	private void displayTriangles(Graphics g, int order, Point p1, Point p2, Point p3) {
		if (order == 0) {
			int[] xPoints = { p1.x, p2.x, p3.x };
			int[] yPoints = { p1.y, p2.y, p3.y };
			g.drawPolygon(xPoints, yPoints, 3);
		} else {
			Point p12 = midpoint(p1, p2);
			Point p23 = midpoint(p2, p3);
			Point p31 = midpoint(p3, p1);
			displayTriangles(g, order - 1, p1, p12, p31);
			displayTriangles(g, order - 1, p12, p2, p23);
			displayTriangles(g, order - 1, p31, p23, p3);
		}
	}

	private Point midpoint(Point p1, Point p2) {
		return new Point((p1.x + p2.x) / 2, (p1.y + p2.y) / 2);
	}

	public static void main(String[] args) {
		JFrame frame = new JFrame("Sierpinski Triangle");
		frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
		SierpinskiTriangle panel = new SierpinskiTriangle();
		frame.add(panel);
		frame.pack();
		frame.setVisible(true);
	}
}

import java.awt.Dimension;

import java.awt.Graphics;

import java.awt.Point;

import javax.swing.JFrame;

import javax.swing.JPanel;

import javax.swing.Timer;

/**

* Sierpinski Dreieck.

* https://de.wikipedia.org/wiki/Fraktal

* https://de.wikipedia.org/wiki/Sierpinski-Dreieck

* @author Thomas Wenzlaff

public class SierpinskiTriangle extends JPanel {

private static final int VERZOEGERUNG_IN_SEKUNDEN = 2000;

private static final long serialVersionUID = 1L;

private int order = 1;

private Timer timer;

public SierpinskiTriangle() {

setPreferredSize(new Dimension(1200, 1200));

timer = new Timer(VERZOEGERUNG_IN_SEKUNDEN, e -> {

order = (order % 10) + 1;

repaint();

});

timer.start();

}

@Override

protected void paintComponent(Graphics g) {

super.paintComponent(g);

Point p1 = new Point(getWidth() / 2, 10);

Point p2 = new Point(10, getHeight() - 10);

Point p3 = new Point(getWidth() - 10, getHeight() - 10);

displayTriangles(g, order, p1, p2, p3);

}

private void displayTriangles(Graphics g, int order, Point p1, Point p2, Point p3) {

if (order == 0) {

int[] xPoints = { p1.x, p2.x, p3.x };

int[] yPoints = { p1.y, p2.y, p3.y };

g.drawPolygon(xPoints, yPoints, 3);

} else {

Point p12 = midpoint(p1, p2);

Point p23 = midpoint(p2, p3);

Point p31 = midpoint(p3, p1);

displayTriangles(g, order - 1, p1, p12, p31);

displayTriangles(g, order - 1, p12, p2, p23);

displayTriangles(g, order - 1, p31, p23, p3);

}

private Point midpoint(Point p1, Point p2) {

return new Point((p1.x + p2.x) / 2, (p1.y + p2.y) / 2);

}

public static void main(String[] args) {

JFrame frame = new JFrame("Sierpinski Triangle");

frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);

SierpinskiTriangle panel = new SierpinskiTriangle();

frame.add(panel);

frame.pack();

frame.setVisible(true);

}