Der Dijkstra-Algorithmus kann das Königsberger Brückenproblem nicht lösen. Aber die Berechnung kürzester Pfade in gewichteten Graphen ist durchaus interessant – zum Beispiel, wenn man wissen möchte, wie man von Frankfurt nach München die kürzeste Strecke findet.
Der Dijkstra-Algorithmus dient der Berechnung des kürzesten Pfads in gewichteten Graphen mit nicht-negativen Kantenlängen.
Dazu schreiben wir ein Java Demo Programm:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 |
package de.wenzlaff.mathe.dijkstra; import java.util.ArrayList; import java.util.Collections; import java.util.List; import java.util.Map; /** * Demo-Programm für den Dijkstra-Algorithmus (Java 21) mit deutschen Städten * als Knoten und Entfernungen in Kilometern. * * Der Graph ist ungerichtet und besitzt nur nicht-negative Kantengewichte. * * Der Algorithmus berechnet die kürzesten Entfernungen von einem Startort * (hier: Frankfurt) zu allen anderen Städten. * * @author Thomas Wenzlaff */ public class CityDijkstraDemo { public static void main(String[] args) { Graph<String> graph = new Graph<>(); // Knoten (Städte) graph.addNode("Frankfurt"); graph.addNode("Mannheim"); graph.addNode("Karlsruhe"); graph.addNode("Augsburg"); graph.addNode("München"); graph.addNode("Würzburg"); graph.addNode("Nürnberg"); graph.addNode("Stuttgart"); graph.addNode("Erfurt"); graph.addNode("Kassel"); // Ungerichtete Kanten mit Entfernungen in km addUndirectedEdge(graph, "Frankfurt", "Mannheim", 85); addUndirectedEdge(graph, "Frankfurt", "Würzburg", 217); addUndirectedEdge(graph, "Frankfurt", "Kassel", 173); addUndirectedEdge(graph, "Mannheim", "Karlsruhe", 80); addUndirectedEdge(graph, "Karlsruhe", "Augsburg", 250); addUndirectedEdge(graph, "Augsburg", "München", 84); addUndirectedEdge(graph, "Würzburg", "Nürnberg", 103); addUndirectedEdge(graph, "Würzburg", "Erfurt", 186); addUndirectedEdge(graph, "Nürnberg", "Stuttgart", 183); addUndirectedEdge(graph, "Nürnberg", "München", 167); addUndirectedEdge(graph, "Kassel", "München", 502); // Startstadt für Dijkstra String start = "Frankfurt"; Map<String, Integer> distanzen = graph.dijkstra(start); Map<String, String> vorgaenger = graph.getPredecessors(); System.out.println("=== Dijkstra-Algorithmus Demo (Start: " + start + ") ==="); System.out.printf("%-12s %-10s %s%n", "Stadt", "Distanz", "Pfad"); System.out.println("----------------------------------------------"); for (String city : graph.getNodes()) { String path = reconstructPath(vorgaenger, start, city); int distance = distanzen.getOrDefault(city, Integer.MAX_VALUE); String distStr = distance == Integer.MAX_VALUE ? "∞" : String.valueOf(distance); System.out.printf("%-12s %-10s %s%n", city, distStr, path); } } /** * Fügt eine ungerichtete Kante ein, indem zwei gerichtete Kanten mit * identischem Gewicht erzeugt werden. */ private static void addUndirectedEdge(Graph<String> graph, String a, String b, int distance) { graph.addEdge(a, b, distance); graph.addEdge(b, a, distance); } /** * Rekonstruiert den Pfad von start nach target anhand der Vorgänger-Map. */ private static String reconstructPath(Map<String, String> predecessors, String start, String target) { if (start.equals(target)) { return start; } if (!predecessors.containsKey(target)) { return "nicht erreichbar"; } List<String> path = new ArrayList<>(); String current = target; while (current != null) { path.add(current); if (current.equals(start)) break; current = predecessors.get(current); } Collections.reverse(path); return String.join(" -> ", path); } } |
Und eine Graph Klasse:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 |
package de.wenzlaff.mathe.dijkstra; import java.util.Comparator; import java.util.HashMap; import java.util.HashSet; import java.util.Map; import java.util.PriorityQueue; import java.util.Set; /** * Einfache gewichtete Graph-Implementierung für Dijkstra. * * @param <T> Typ der Knotenschlüssel (z.B. String) * * @author Thomas Wenzlaff */ class Graph<T> { private final Map<T, Map<T, Integer>> adjacency = new HashMap<>(); private Map<T, T> predecessors = new HashMap<>(); public void addNode(T node) { adjacency.putIfAbsent(node, new HashMap<>()); } /** * Fügt eine gerichtete Kante mit ganzzahligem Gewicht hinzu. */ public void addEdge(T source, T target, int weight) { if (weight < 0) { throw new IllegalArgumentException("Negative Gewichte sind nicht erlaubt"); } addNode(source); addNode(target); adjacency.get(source).put(target, weight); } /** * Dijkstra-Algorithmus: berechnet kürzeste Entfernungen vom Startknoten. * * @param start Startknoten * @return Map mit minimalen Distanzen zu allen Knoten */ public Map<T, Integer> dijkstra(T start) { Map<T, Integer> dist = new HashMap<>(); predecessors = new HashMap<>(); Set<T> visited = new HashSet<>(); for (T node : adjacency.keySet()) { dist.put(node, Integer.MAX_VALUE); } dist.put(start, 0); record Entry<T>(T node, int distance) { } PriorityQueue<Entry<T>> pq = new PriorityQueue<>(Comparator.comparingInt(Entry::distance)); pq.add(new Entry<>(start, 0)); while (!pq.isEmpty()) { Entry<T> currentEntry = pq.poll(); T u = currentEntry.node; if (!visited.add(u)) { continue; } int du = dist.get(u); if (du == Integer.MAX_VALUE) { continue; } for (Map.Entry<T, Integer> edge : adjacency.get(u).entrySet()) { T v = edge.getKey(); int weight = edge.getValue(); int alt = du + weight; if (alt < dist.getOrDefault(v, Integer.MAX_VALUE)) { dist.put(v, alt); predecessors.put(v, u); pq.add(new Entry<>(v, alt)); } } } return dist; } public Set<T> getNodes() { return adjacency.keySet(); } public Map<T, String> getStringPredecessors() { Map<T, String> map = new HashMap<>(); for (Map.Entry<T, T> e : predecessors.entrySet()) { map.put(e.getKey(), e.getValue().toString()); } return map; } public Map<T, T> getPredecessors() { return predecessors; } } |
Das Ergebnis nach der Ausführung in Eclipse:

Der Code ist auch in meinem GitLab-Repo zu finden.
Jahrelang hat man gedacht, das der Dijkstra-Algorithmus die schnellste Lösung des Problems ist. Das mathematische Tempolimit, in den Quellen als Sortierschranke (sorting barrier) bezeichnet, galt seit dem Jahr 1984.
In diesem Jahr gelang es dem Informatiker Robert Tarjan zusammen mit einem Kollegen, den klassischen Dijkstra-Algorithmus so weit zu optimieren, dass er genau an diese theoretische Grenze stieß. Vor kurzem hat man dann eine bahnbrechende Entdeckung gemacht, es geht doch schneller wie in A New Algorithm Makes It Faster to Find the Shortest Paths gezeigt.
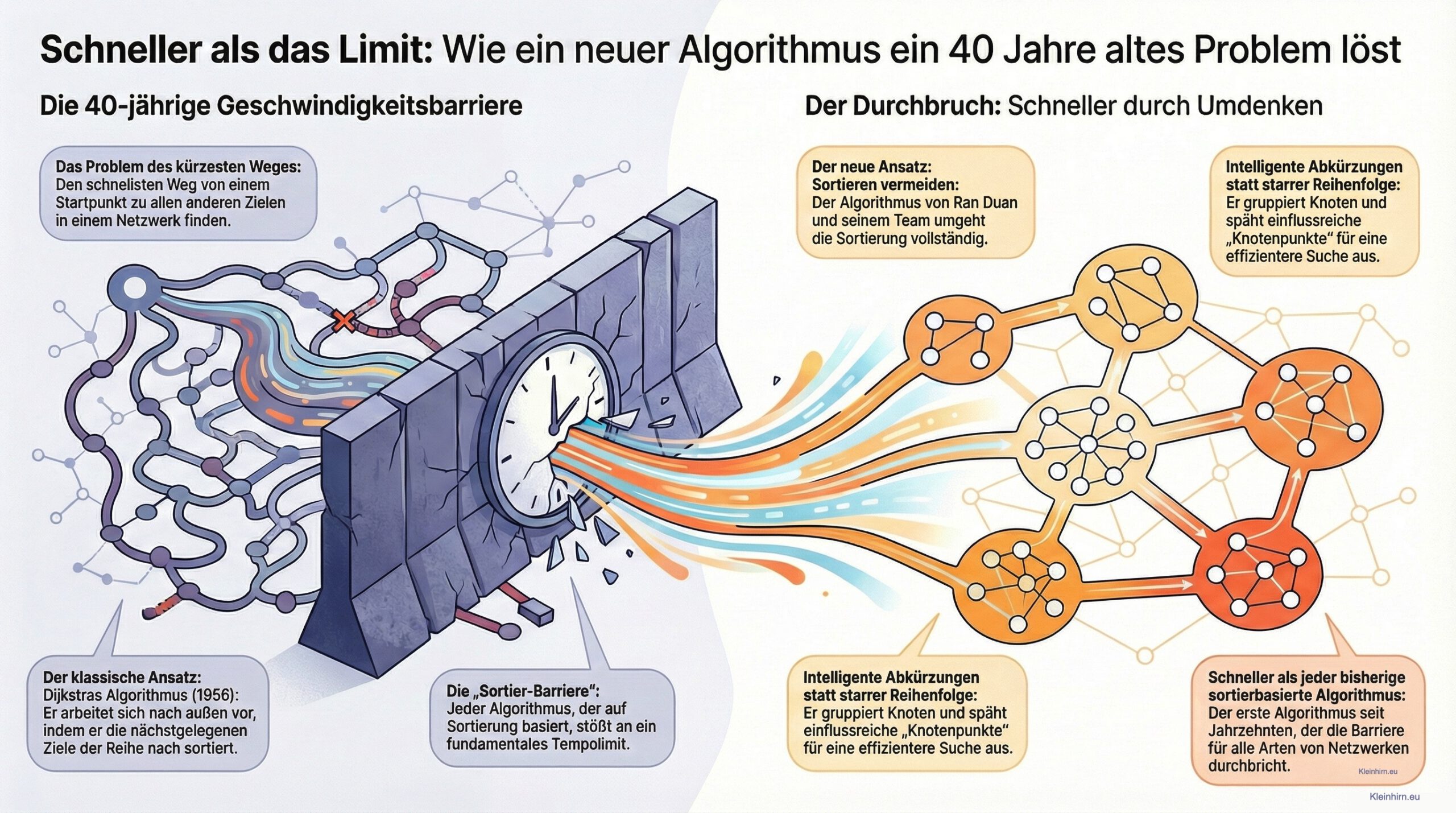
Dieser Artikel beschreibt einen bedeutenden Durchbruch in der Informatik, bei dem Forscher eine vierzig Jahre alte Geschwindigkeitsbarriere für Kürzeste-Wege-Algorithmen durchbrochen haben. Während klassische Methoden wie der Dijkstra-Algorithmus durch die notwendige Sortierung von Distanzen begrenzt waren, nutzt das neue Team um Ran Duan innovative Gruppierungstechniken. Durch die gezielte Identifizierung einflussreicher Knotenpunkte umgeht das Verfahren die Sortierschranke und arbeitet effizienter auf komplexen Graphen.
Zusammenfassend lässt sich sagen: Während der aktuelle messbare Geschwindigkeitsvorteil gegenüber der optimierten Dijkstra-Variante eher klein ist, ist der theoretische Unterschied gigantisch, da er beweist, dass das bisherige mathematische Gesetz zur Höchstgeschwindigkeit für diese Art von Problemen nicht mehr gilt.
Man kann sich das wie das Durchbrechen der Schallmauer vorstellen: Es geht nicht nur darum, ein paar Stundenkilometer schneller zu sein als das bisher schnellste Flugzeug, sondern darum, eine physikalische Grenze überwunden zu haben, die zuvor als absolut galt, und damit den Weg für eine völlig neue Generation von Triebwerken zu ebnen. Ich bin gespannt was da noch kommt.
