Der Diffie-Hellman-Schlüsselaustausch ist ein Weg, wie zwei Menschen einen geheimen Schlüssel finden können, ohne ihn direkt hin- und herzuschicken.
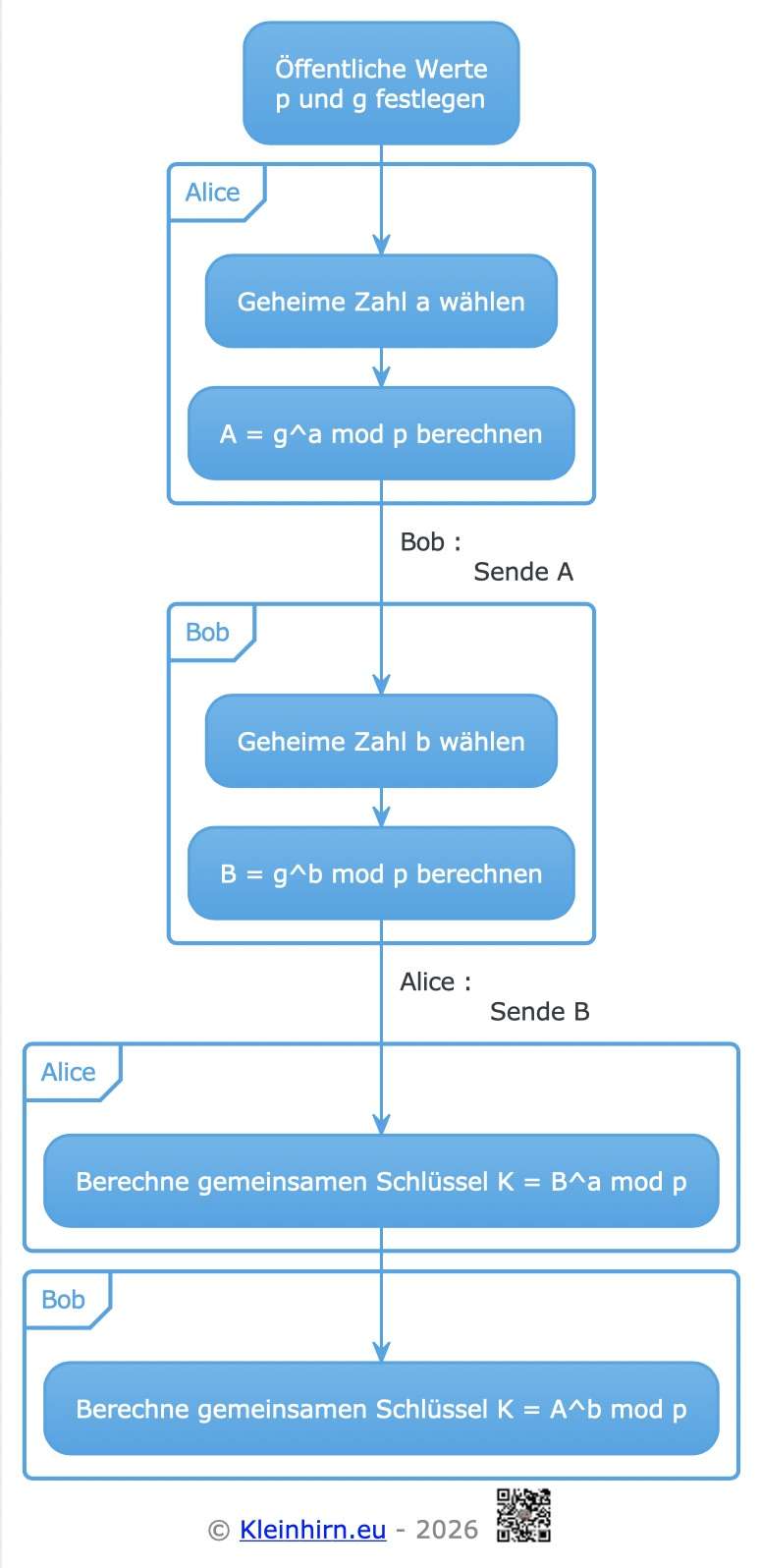
Zuerst einigen sie sich öffentlich auf eine große Zahl (eine Primzahl) und eine Basiszahl.
Jeder wählt dann eine geheime Zahl für sich selbst. Mit der geheimen Zahl rechnen sie eine neue Zahl aus, die sie dem anderen schicken.
Danach kann jeder mit der Zahl vom anderen und seiner eigenen geheimen Zahl denselben geheimen Schlüssel berechnen. Und zwar so:
Einfach gesagt und ein Beispiel in Java:
– Alice und Bob einigen sich auf eine große Primzahl und eine Basis . Beide Zahlen sind für jeden sichtbar
– Alice nimmt ihre geheime Zahl und rechnet A = g^a \mod p aus. Die Zahl schickt sie an Bob
– Bob macht das Gleiche mit seiner geheimen Zahl und berechnet B = g^b \mod p . Die Zahl schickt er an Alice
– Alice benutzt und ihre geheime Zahl , um den gemeinsamen Schlüssel zu berechnen: K = B^a \mod p
– Bob benutzt und seine geheime Zahl , um den Schlüssel zu berechnen: K = A^b \mod p
Am Ende haben beide den gleichen geheimen Schlüssel, obwohl jeder seine geheime Zahl für sich behalten hat.
Ein fremder Lauscher kann diesen Schlüssel praktisch nicht herausfinden. Deshalb kann der Schlüssel sicher zum Verschlüsseln verwendet werden.
Man nennt das Verfahren auch Schlüsselvereinbarung, weil beide auf sichere Weise denselben Schlüssel finden, ohne ihn direkt zu tauschen (siehe auch Wikipedia)
Hier nun noch ein einfaches Beispiel in Java:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
package de.wenzlaff.crypto; import java.math.BigInteger; import java.security.SecureRandom; /** * Hier ist ein einfaches Java-Programm zur Demo, das den * Diffie-Hellman-Schlüsselaustausch demonstriert. * * Es verwendet die Java-eigene Klasse BigInteger für große Zahlen und zeigt, * wie Alice und Bob ihre geheimen Schlüssel berechnen und austauschen, um zum * gleichen gemeinsamen Schlüssel zu kommen. * * Dieses Programm zeigt die einzelnen Schritte des Diffie-Hellman-Verfahrens * mit exemplarisch kleinen Zahlen für bessere Verständlichkeit. In der Praxis * sollten die Werte von und deutlich größer sein (> 3000 Bit) für Sicherheit. * Der geheime Schlüssel ist das Ergebnis, das sowohl Alice als auch Bob * berechnen und das gleich ist. Der Wert wird hier nur ausgegeben, aber könnte * z.B. als symmetrischer Schlüssel für Verschlüsselung genutzt werden. * * @author Thomas Wenzlaff * */ public class DiffieHellmanKeyTausch { public static void main(String[] args) { // Öffentliche Parameter: große Primzahl p und Generator g // p ist eine große Primzahl, die als Modul für alle Berechnungen dient. Sie // definiert die “Ringgröße” für die modularen Potenz-Rechnungen. Die Wahl von // ist entscheidend für die Sicherheit, denn sie muss so groß sein, dass der // diskrete Logarithmus (also das Auffinden geheimer Exponenten) praktisch nicht // lösbar ist. Typischerweise wird eine mit mehreren hundert oder tausend Bit // Länge gewählt. BigInteger p = new BigInteger("23"); // kleine Primzahl als Beispiel, in der Praxis viel größer // g ist eine sogenannte Primitivwurzel modulo, auch Generator genannt. Das // bedeutet, dass die Potenzen von modulo alle Zahlen von 1 bis p -1 // erzeugen können. // Es ist also ein Basiswert, mit dem die geheimen Zahlen potenziert werden, um // öffentliche Schlüssel zu generieren. BigInteger g = new BigInteger("5"); // Generator (Basiswert für Potenzierung modulo ) SecureRandom random = new SecureRandom(); // Alice wählt ihre geheime Zahl a BigInteger a = new BigInteger(5, random); // zufällige Zahl kleiner 2^5 (als Beispiel) // Bob wählt seine geheime Zahl b BigInteger b = new BigInteger(5, random); System.out.println("Öffentliche Parameter:"); System.out.println("p = " + p); System.out.println("g = " + g); System.out.println("\nAlice wählt geheime Zahl a = " + a); System.out.println(" Bob wählt geheime Zahl b = " + b); // Alice berechnet A = g^a mod p BigInteger A = g.modPow(a, p); // berechnet den modularen Exponent // Bob berechnet B = g^b mod p BigInteger B = g.modPow(b, p); System.out.println("\nAlice berechnet und sendet A = g^a mod p = " + g + "^" + a + " mod " + p + " = " + A); System.out.println(" Bob berechnet und sendet B = g^b mod p = " + g + "^" + b + " mod " + p + " = " + B); // Alice berechnet geheimen Schlüssel K = B^a mod p BigInteger keyAlice = B.modPow(a, p); // Bob berechnet geheimen Schlüssel K = A^b mod p BigInteger keyBob = A.modPow(b, p); System.out.println("\nAlice berechnet gemeinsamen Schlüssel: " + keyAlice); System.out.println(" Bob berechnet gemeinsamen Schlüssel: " + keyBob); // Prüfen, dass beide Schlüssel gleich sind System.out.println("\nSchlüssel stimmen überein: " + keyAlice.equals(keyBob)); } } |
Beispiel Ausgabe:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Öffentliche Parameter: p = 23 g = 5 Alice wählt geheime Zahl a = 2 Bob wählt geheime Zahl b = 13 Alice berechnet und sendet A = g^a mod p = 5^2 mod 23 = 2 Bob berechnet und sendet B = g^b mod p = 5^13 mod 23 = 21 Alice berechnet gemeinsamen Schlüssel: 4 Bob berechnet gemeinsamen Schlüssel: 4 Schlüssel stimmen überein: true |
