In der Informationssicherheit und Verschlüsselung steht „CA“ für Certification Authority. Eine Zertifizierungsstelle ist eine vertrauenswürdige Organisation, die digitale Zertifikate ausstellt und verwaltet. Diese Zertifikate werden verwendet, um die Identität von Websites, Servern und Benutzern in verschlüsselten Kommunikationen zu überprüfen, z. B. bei der SSL/TLS-Verschlüsselung im Web. Hier ein Bild der XCA GUI unter Linux:
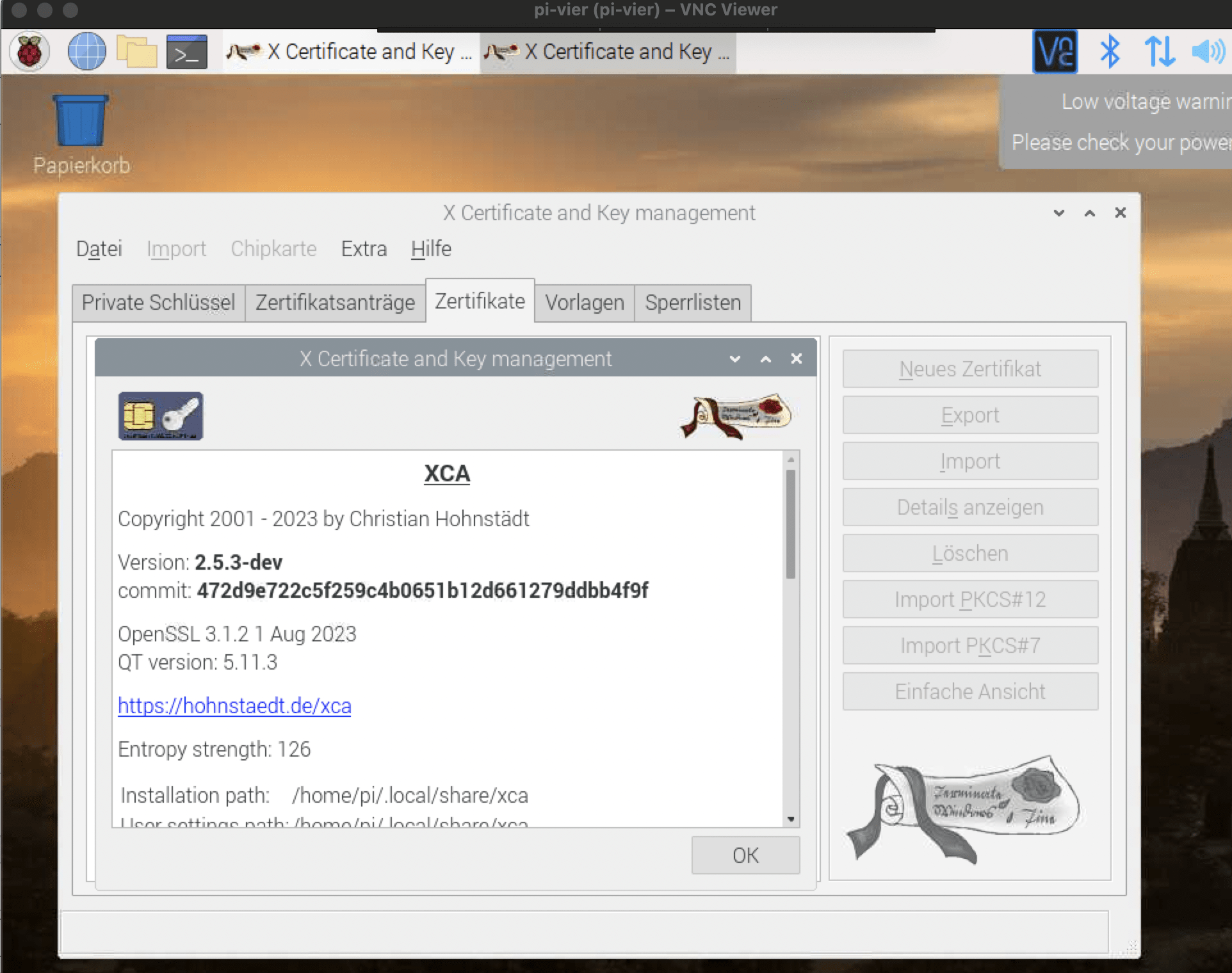
Gestern wurde eine neue Version 2.5.0 der XCA veröffentlicht. Dafür gibt es auf dem Raspberry Pi 4 noch kein Package.
Aber man kann es ja auch selbst compilieren und zwar so für den aktuellen dev 2.5.3 Stand:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# Abhängigkeiten installieren # für Bookworm sudo apt install build-essential libssl-dev pkg-config qtbase5-dev qttools5-dev-tools libqt5sql5 libqt5help5 cmake qttools5-dev python3-sphinxcontrib.qthelp # für Bullseye oder Buster sudo apt install build-essential libssl-dev pkg-config qtbase5-dev qttools5-dev-tools libqt5sql5 libqt5help5 cmake qttools5-dev python3-sphinx # Projekt clonen git clone https://github.com/chris2511/xca.git # Konfigurieren cmake -B build xca # Bauen, ca eine halbe Stunde auf dem Pi 4 cmake --build build -j5 # Installieren sudo cmake --install build # Aufrufen und Test siehe http://blog.wenzlaff.de/?p=20761 |
Es gibt nun viele EC Keys, hier eine Auswahl:

Oder auch alle 79, über die CMD mit: xca –list-curves
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
secp112r1 SECG/WTLS curve over a 112 bit prime field secp112r2 SECG curve over a 112 bit prime field secp128r1 SECG curve over a 128 bit prime field secp128r2 SECG curve over a 128 bit prime field secp160k1 SECG curve over a 160 bit prime field secp160r1 SECG curve over a 160 bit prime field secp160r2 SECG/WTLS curve over a 160 bit prime field secp192k1 SECG curve over a 192 bit prime field secp224k1 SECG curve over a 224 bit prime field secp224r1 NIST/SECG curve over a 224 bit prime field secp256k1 SECG curve over a 256 bit prime field secp384r1 NIST/SECG curve over a 384 bit prime field secp521r1 NIST/SECG curve over a 521 bit prime field prime192v1 NIST/X9.62/SECG curve over a 192 bit prime field prime192v2 X9.62 curve over a 192 bit prime field prime192v3 X9.62 curve over a 192 bit prime field prime239v1 X9.62 curve over a 239 bit prime field prime239v2 X9.62 curve over a 239 bit prime field prime239v3 X9.62 curve over a 239 bit prime field prime256v1 X9.62/SECG curve over a 256 bit prime field sect113r1 SECG curve over a 113 bit binary field sect113r2 SECG curve over a 113 bit binary field sect131r1 SECG/WTLS curve over a 131 bit binary field sect131r2 SECG curve over a 131 bit binary field sect163k1 NIST/SECG/WTLS curve over a 163 bit binary field sect163r1 SECG curve over a 163 bit binary field sect163r2 NIST/SECG curve over a 163 bit binary field sect193r1 SECG curve over a 193 bit binary field sect193r2 SECG curve over a 193 bit binary field sect233k1 NIST/SECG/WTLS curve over a 233 bit binary field sect233r1 NIST/SECG/WTLS curve over a 233 bit binary field sect239k1 SECG curve over a 239 bit binary field sect283k1 NIST/SECG curve over a 283 bit binary field sect283r1 NIST/SECG curve over a 283 bit binary field sect409k1 NIST/SECG curve over a 409 bit binary field sect409r1 NIST/SECG curve over a 409 bit binary field sect571k1 NIST/SECG curve over a 571 bit binary field sect571r1 NIST/SECG curve over a 571 bit binary field c2pnb163v1 X9.62 curve over a 163 bit binary field c2pnb163v2 X9.62 curve over a 163 bit binary field c2pnb163v3 X9.62 curve over a 163 bit binary field c2pnb176v1 X9.62 curve over a 176 bit binary field c2tnb191v1 X9.62 curve over a 191 bit binary field c2tnb191v2 X9.62 curve over a 191 bit binary field c2tnb191v3 X9.62 curve over a 191 bit binary field c2pnb208w1 X9.62 curve over a 208 bit binary field c2tnb239v1 X9.62 curve over a 239 bit binary field c2tnb239v2 X9.62 curve over a 239 bit binary field c2tnb239v3 X9.62 curve over a 239 bit binary field c2pnb272w1 X9.62 curve over a 272 bit binary field c2pnb304w1 X9.62 curve over a 304 bit binary field c2tnb359v1 X9.62 curve over a 359 bit binary field c2pnb368w1 X9.62 curve over a 368 bit binary field c2tnb431r1 X9.62 curve over a 431 bit binary field wap-wsg-idm-ecid-wtls1 WTLS curve over a 113 bit binary field wap-wsg-idm-ecid-wtls3 NIST/SECG/WTLS curve over a 163 bit binary field wap-wsg-idm-ecid-wtls4 SECG curve over a 113 bit binary field wap-wsg-idm-ecid-wtls5 X9.62 curve over a 163 bit binary field wap-wsg-idm-ecid-wtls6 SECG/WTLS curve over a 112 bit prime field wap-wsg-idm-ecid-wtls7 SECG/WTLS curve over a 160 bit prime field wap-wsg-idm-ecid-wtls8 WTLS curve over a 112 bit prime field wap-wsg-idm-ecid-wtls9 WTLS curve over a 160 bit prime field wap-wsg-idm-ecid-wtls10 NIST/SECG/WTLS curve over a 233 bit binary field wap-wsg-idm-ecid-wtls11 NIST/SECG/WTLS curve over a 233 bit binary field wap-wsg-idm-ecid-wtls12 WTLS curve over a 224 bit prime field brainpoolP160r1 RFC 5639 curve over a 160 bit prime field brainpoolP160t1 RFC 5639 curve over a 160 bit prime field brainpoolP192r1 RFC 5639 curve over a 192 bit prime field brainpoolP192t1 RFC 5639 curve over a 192 bit prime field brainpoolP224r1 RFC 5639 curve over a 224 bit prime field brainpoolP224t1 RFC 5639 curve over a 224 bit prime field brainpoolP256r1 RFC 5639 curve over a 256 bit prime field brainpoolP256t1 RFC 5639 curve over a 256 bit prime field brainpoolP320r1 RFC 5639 curve over a 320 bit prime field brainpoolP320t1 RFC 5639 curve over a 320 bit prime field brainpoolP384r1 RFC 5639 curve over a 384 bit prime field brainpoolP384t1 RFC 5639 curve over a 384 bit prime field brainpoolP512r1 RFC 5639 curve over a 512 bit prime field brainpoolP512t1 RFC 5639 curve over a 512 bit prime field |
Auch meine Lieblingskurve secp256k1 ist dabei.
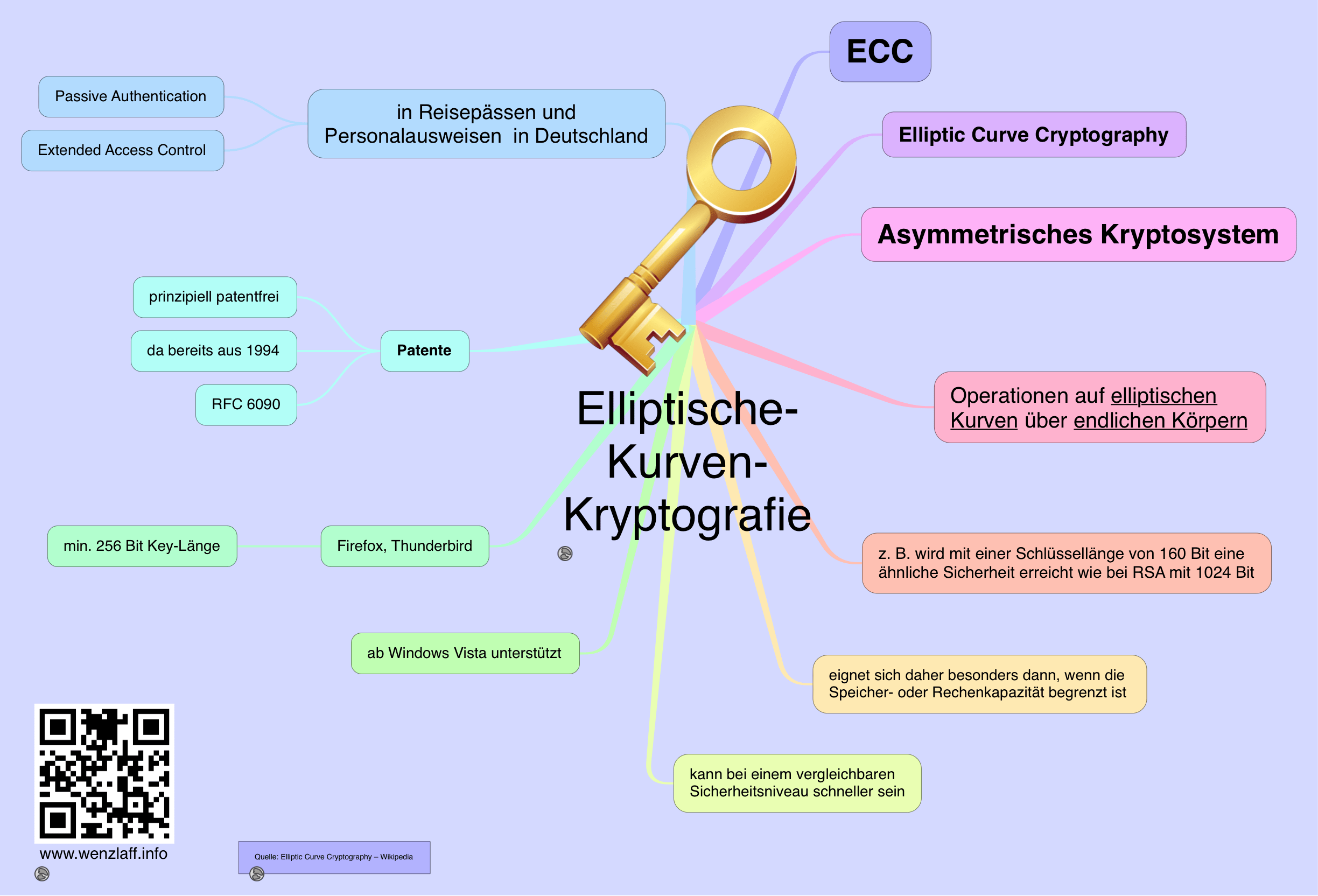
Die Elliptische-Kurven-Kryptografie (ECC) ist eine moderne Form der Public-Key-Kryptografie, die auf der mathematischen Theorie elliptischer Kurven basiert. Die ECC wird häufig für die sichere Verschlüsselung von Daten und digitale Signaturen in verschiedenen Anwendungen, einschließlich Kryptowährungen wie Bitcoin, verwendet. Die ECC ist effizienter als viele andere Public-Key-Kryptosysteme und bietet eine vergleichbare Sicherheit bei kürzeren Schlüssellängen, was zu einer geringeren Rechenleistung und einem geringeren Speicherbedarf führt.
